Lesson 11: Discover 2 | MoodleHUB 🎓

1. Lesson 11

1.2. Discover 2

Module 2: Lesson 11

Module 2: Logic and Geometry

Try This 1

Based on your findings from the Interior Angles of Polygons applet, make a conjecture about the relationship between the sum of the measures of the interior angles of a polygon, S, and the number of sides of the polygon, n.
Use your conjecture from question 1 to predict the sum of the measures of the interior angles of a tridecagon (i.e., 13 sides). Verify your prediction using triangles.

Self-Check 1

Complete “Check Your Understanding” question 3 on page 99 of your textbook. Answer

An understanding of the properties of angles of polygons is also helpful when creating puzzles such as tangrams. Invented in China between 1796 and 1802, a tangram is a seven-piece puzzle. The objective of the puzzle is to create a specific shape using all seven pieces provided without allowing any of the pieces to overlap.

Did You Know?

This is a photo of a tangram puzzle in a wooden box.

Tangrams started the world’s first puzzle craze almost 200 years ago. Napoleon Bonaparte, Lewis Carroll, Edgar Allan Poe, Hans Christian Anderson, and Michael Faraday are just some of the international celebrities who amused themselves with the tangram. Want to try out a tangram? Tangrams are available online or as an app for your favourite handheld device. A search of “tangram” or “tangram games” using an Internet search engine will provide a variety of selections.

— Adapted from Erik D. Demaine. A Lifetime of Puzzles. (London: AK Peters, 2008), p.59.

exterior angle of a polygon: an angle at a vertex of the polygon, on the outside of the polygon, formed by one side and the extension of an adjacent side

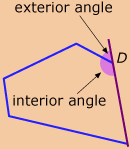
This illustration shows an interior angle and an exterior angle in a polygon.

Interior angles are not the only angles that need to be considered when arranging polygons in a tile design or to solve a puzzle. To ensure that different shapes and sizes of tiles align as planned, an understanding of the exterior angles of a polygon is also required.

An exterior angle of a polygon is an angle formed by a side and an extension of an adjacent side. In Lesson 9 you learned that exterior angles and their adjacent interior angles are supplementary. The angles lie on a straight line, so their sum is 180°. You also showed that the measure of an exterior angle of a triangle is equal to the sum of the measures of the non-adjacent interior angles.

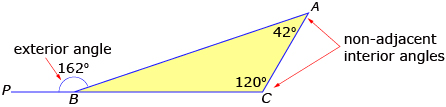
This illustration shows two non-adjacent interior angles and an exterior angle in a triangle.

sum of exterior angle = sum of measures of the non-adjacent interior angles

162° = 42° + 120°

You have looked at how the number of sides in a polygon is related to the sum of its interior angles. Now you will look at how the number of sides in a polygon is related to the sum of its exterior angles.