Module 1
1. Module 1
1.4. Page 4
Module 1: The International System of Units (SI)
Bringing Ideas Together
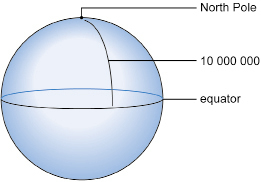
When SI was first developed in France over 200 years ago, the metre was defined as one ten-millionth of the distance from the North Pole to the equator.
Did You Know?
Today, because of the precision required in science and industry, the metre is defined as the distance light travels in a vacuum in the time interval of 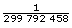 of a second.
of a second.
In SI, prefixes are used to represent multiples or fractions of the base unit.
- Add the prefix kilo to metre, and you have the kilometre.
- Add the prefix centi to metre, and you have the centimetre.
- Add the prefix milli to metre, and you have the millimetre.
The prefixes kilo, centi, and milli are the most common and are bolded, along with their symbols, in the following table of SI prefixes.
|
Prefix |
Symbol |
Factor |
|
mega |
M |
1 000 000 or 106 |
|
kilo |
k |
1000 or 103 |
|
hecto |
h |
100 or 102 |
|
deca |
da |
10 or 101 |
|
— |
— |
1 or 100 |
|
deci |
d |
0.1 or 10–1 |
|
centi |
c |
0.01 or 10–2 |
|
milli |
m |
0.001 or 10–3 |
|
micro |
µ |
0.000 001 or 10–6 |
 Try This
Try This
In comparing SI units to each other, the prefixes are important. Play “Prefix Matching Game” to help you quickly recognize and order the prefixes based on the factor they represent.
Prefixes in SI

© Stephen Coburn/shutterstock
For length, the most common prefixes you will generally encounter are milli, centi, and kilo. What are the symbols for millimetre, centimetre, metre, and kilometre? You may recall working with the symbols mm, cm, m, and km in previous math courses.
Have you seen the prefixes milli, centi, and kilo used with volume? In your course folder, record examples of these prefixes used to describe volumes you encounter during the day. In Lesson 3 you will explore volumes using these prefixes.
 Try This
Try This
In the Explore section of this lesson, you converted between SI units for measurement. This showed how powers of 10 are involved in converting between units. You must be able to convert quickly among these units by applying your skills with powers of 10.
Fortunately, because only powers of 10 are involved, SI unit conversion only involves the movement of the decimal. Open “SI Length Conversion” to see this conversion.
In this multimedia piece, drag the left slider, connected to a moveable box, up or down to match the units you have in a given measurement. Enter the numeric part of the measurement into the moveable box. Then drag the right slider to match the units into which you want to convert the measurement.
Still using “SI Length Conversion,” convert a distance of 500 m to kilometres (km). Using mental math, you may be able to predict that the conversion should show this measurement as 0.500 km. See that it does. Try several other conversions so that you are comfortable with this procedure.
TT 6. Make a rule that allows you to predict which direction you must move the decimal place when making unit conversions.
Write your rule in your course folder. Your teacher may look at your work in order to monitor your learning.
 Self-Check
Self-Check
SC 5. Complete a table like this one, then check your answers.
|
1 km = ? m |
1 m = ? km |
|
1 m = ? cm |
1 cm = ? m |
|
1 m = ? mm |
1 mm = ? m |
|
1 cm = ? mm |
1 mm = ? cm |

Estimating lengths and distances in SI is a useful skill. To estimate, it helps to visualize the size of some SI units. A millimetre is about the thickness of a dime, and a centimetre is about the width of your little finger. What everyday objects are about the length of a metre? A kilometre is the distance you can walk in about ten minutes.
Because you are working with powers of 10, you simply move the decimal point to convert between units. Work though several examples with your teacher or study partner.
Example 1

Coin image © 2010 Royal Canadian Mint – All Rights Reserved /
Image de pièce© 2010 Monnaie royale canadienne – Tous droits réservés
A two-dollar coin is approximately 28 mm in diameter.
- What is the width in centimetres (cm)?
- What is the width in metres (m)?
Solution
- Since 1 mm = 0.1 cm, multiply 28 mm by 0.1 or 10–1.

Can you suggest another way of doing the problem?

- Since 1 mm = 0.001 m, multiply 28 mm by 0.001 or 10–3.
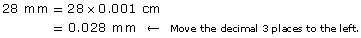
Example 2
Yin lives 2.5 km from school. Convert that distance to metres.
Solution
Since 1 km = 1000 m, multiply 2.5 km by 1000 or 103.

Example 3
Jon’s height printed on his driver’s licence is 162 cm. What is his height in metres?
Solution
Since 1 cm = 0.01 m, multiply 162 cm by 0.01 or 10–2.
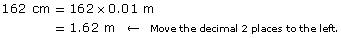
 Self-Check
Self-Check
SC 6. The local golf course is 6750 m in length. What is the length of this course in kilometres (km)?
SC 7. A roadside sign indicates a school-bus stop in 0.3 km. How far is the sign from the bus stop in metres?
SC 8. The length and width of a stamp are most often expressed in millimetres. Why?
SC 9. A package of 500 sheets of printer paper is 5 cm thick. How thick is a single sheet in metres?
SC 10.The height of the walls in Shawna’s room is 2.4 m. What is the height in centimetres?
SC 11. A letter-size sheet of copy paper is 216 mm by 279 mm. What are its dimensions in centimetres?
SC 12. Andrey Alexandrovich Silnov, of Russia, won the 2008 men’s high jump gold medal in the 2008 Olympics with a leap of 2.36 m. What was his achievement in centimetres?
SC 13. Inuit culture has existed since 1000 AD in Northern Canada and Alaska. The Inuit made toy sleds out of ivory and wood for their children. These toys taught their children about proper sled construction—a key skill in the frozen north!

What are the dimensions of the toy Inuit sled in millimetres?
SC 14. Anya, in Newfoundland, found an arrowhead from the Beothuks. Being curious, she researched her find and discovered it was not an arrowhead but the head of a sealing harpoon. Anya discovered that the Beothuks hunted seal by pursuing them in human-propelled boats (known as kayaks today). They made their catch by throwing harpoons (with rope attached) at their prey.

The harpoon head is made from flint and is 44.5 mm long. What is the length of this harpoon head in centimetres?
SC 15. The school running track is oval in shape and is 200 m in circumference. How many times must a runner go around the track to run 1.6 km?
 Mastering Concepts
Mastering Concepts
Try this question. When you are finished, check your answer.
The orbit of Earth around the sun is not circular. The distance from Earth to the sun changes as it travels around the sun. The closest Earth is from the sun is about 1.46 × 1011 m. The farthest Earth is from the sun is about 1.52 × 1011 m.
What is the difference between these distances in kilometres?
Express your answer in standard (everyday) notation. For example, 3.2 × 102 is a number in scientific notation. If instead of using 102, you move the decimal two places to the right, the result, 320, is in standard notation.