Module 1
1. Module 1
1.7. Page 2
Module 1: The International System of Units (SI)
Get Started

© Germán Ariel Berra/shutterstock
Suppose you wanted to describe the areas of a postage stamp, the front of your MP3 player, a living-room carpet, and a buffalo paddock. Could you use your thumbprints to describe the area of any of these?
For the carpet and the paddock, you would need an area unit much larger than a thumbprint. If you chose an appropriate area unit, you could cover the carpet or paddock with a specific number of area units that would be easy to express and understand.
 Try This
Try This
In this activity you will use your thumbprints to see how area units can be used to measure the area of a surface.
You will need a sheet of plain paper, like the paper you would use in a computer printer. In order to leave a record of your thumbprints, you will dip your thumb in cooking oil or a diluted mixture of food dye. You could also just use a pencil to outline the positions of your thumb on the sheet of paper.
Step 1: On your piece of paper, apply a method to give the approximate number of thumbprints you can fit on the sheet of paper.
TT 1. Approximately how many of your thumbprints cover the sheet of paper?
TT 2. Describe a method you used to find the approximate number of thumbprints you could fit on the sheet of paper.
TT 3. Based on your findings, what is the area of the sheet of paper in thumbprints?
Place a copy of your answers in your course folder.
Unit Squares
Your thumbprint is rounded and not square, so there is always some surface left uncovered between the thumbprints. You will remember from your earlier work that area is the number of unit squares needed to cover a surface. Unit squares can cover a surface without leaving any exposed space between the squares. That’s one reason why unit squares—rather than rounded unit shapes—are used to measure area.
Suppose a rectangular sheet is 4 units long and 3 units wide. A grid of lines is drawn over the sheet to make the dimensions and area visible. What is the area of this rectangular sheet?

How many unit squares cover this rectangle? Did you count the total number of squares, or did you remember a shortcut method based on multiplication?
Suppose a sheet is square, having a side length of 3 units. What is the area of this square sheet?
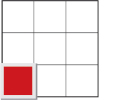
How can you use multiplication to determine the area of this square and any other square?