1. Lesson 1

1.4. Discover

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

 
Discover

 

Did You Know?



A quad is a four-wheel, all-terrain vehicle used for exploring the outdoors and having fun. Quad means “four.” But a quadratic relation has a variable taken only to the second power or, in other words, squared. The simplest example of a quadratic function is y = x2 or, as it is sometimes written, f(x) = x2. Where does the four come in?

 

This shows a photo of a quad jumping into the air.

iStockphoto/Thinkstock

 

The name came from having to find the area of the regular quadrilateral (four-sided figure) called a square. To determine the area of the square, you square the length of a side (s2) or multiply the length by itself (s × s).



Relations are rules that connect one value to another. Relations can be described as ordered pairs in which the first value is the input and the second value is the output. They can also be described in a table of values or using graphs.

 

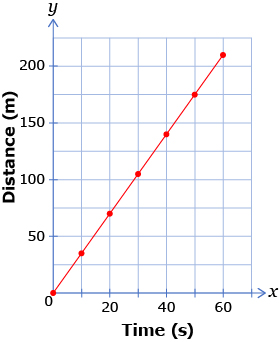
Many different situations can be modelled by relations. For example, the linear relation y = 3.5x could be used to model the movement of a quad travelling at a constant speed of 3.5 m/s over a given period of time.

 

Time (s)

0

10

20

30

40

50

60

Distance (m)

0

35

70

105

140

175

210


This is a distance time graph for a quad that is travelling at a constant speed of 3.5 m/s for 60 seconds.

 

Likewise, the path of the quad in a jump can be modelled by a quadratic relation. For example, the quadratic relation y = −5x2 + 10x describes the path of a quad during a jump where the variable y represents the height of the quad above the ground and the variable x represents time.

 

x

0

0.5

1

1.5

2

y

0

3.75

5

3.75

0

This is a graph shaped like a parabola that goes through (0, 0), (0.5, 3.75), (1, 5), (1.5, 3.75), and (2, 0).

 

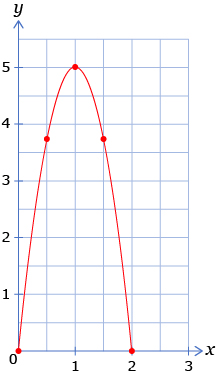
parabola: the curve-shaped graph of a quadratic relation

Notice that the graph of a linear relation is a straight line, whereas the shape of the graph of a quadratic relation is a parabola. All quadratic relations have a variable raised to the second power. Thus, all quadratic relations have a degree of 2.

 

For example, only one of the following functions is a quadratic function. Only one function has 2 as the highest power of the variable. If there is an exponent higher than 2 in the function, it is not a quadratic function.

 

 
f(x) = 2x + 5 This is a linear function—can be written as y = mx + b.
y = −0.2x + 5x + 4 This is a linear function—can be written as y = mx + b.
f(x) = 3x3 + 5x2 + 2x + 9 The highest power is 3, so this is not a quadratic function.
y = 3x2 + 6 This is a quadratic function. (2 is the highest power of the variable.)

 

Watch the video Exploring Parabolas and Polynomial Equations. Click the “Interactive” button to see other examples of quadratic relations that are used to study the flight path of objects.

 

 

This is a screenshot for Exploring Parabolas and Polynomial Equations.