1. Module 1

1.14. Page 4

Mathematics 10-3 Module 1 Lesson 3

Module 1: The International System of Units (SI)

 

Bringing Ideas Together

 

In the Explore section, the volume of sugar each container held was given by the number of cubes of sugar. This is how all volumes are expressed—as the number of cubic units of space something occupies.

 

Remember, the volume of a rectangular box is found using the following formula:

 

 

 

volume = length × width × height

V = l × w × h

 

One commonly used unit of volume in SI is the cubic metre (m3).

 

This drawing shows a cube having edges measuring 1 m.

 

Now you will look at putting these linear units to work finding volumes.

 

Example 1

 

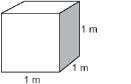
What is the volume in m3 of a rectangular box 60 cm long, 50 cm wide, and 40 cm high?

 

Solution

 

Because the volume is asked for in m3, convert the dimensions of the box to metres.

 

 

 

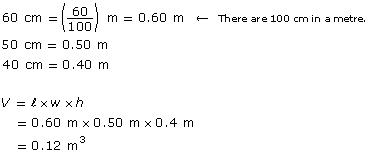
eqn052.eps

 

Small Units of Volume

 

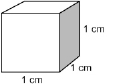
Another common unit of volume is the cubic centimetre (cm3). The cubic centimetre is used for smaller objects, such as the volume of a milk container or the volume of a jewel.

 

This drawing shows a cube having sides measuring 1 cm long.

 

Did You Know?

 

Did you know the cubic centimetre is often referred to as the millilitre?

The cubic centimetre is much smaller than a cubic metre. How many cubic centimetres are there in a cubic metre?

 

 

 

 

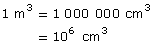
The interactive “SI Volume Conversion” can be used to show the conversion between units.

 

For example, by positioning the left slider next to m3 and the right slider to cm3 you can see that 1 m3 = 1 000 000 cm3 without doing any calculation. You can also use “SI Volume Conversion” to confirm the solutions in the examples, in the Self-Check questions that follow, and anywhere else you need to make volume conversions.

 

Example 2

 

Convert 0.12 m3 to cubic centimetres.

 

Solution

 

 

 

 

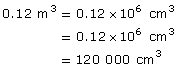
Recall from the previous example that 0.12 m3 was the volume of the rectangular box that measured 60 cm × 50 cm × 40 cm. You could have found the volume in cubic centimetres directly.

 

 

 

 

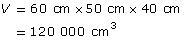
Either calculation gives the same value.

 

m10_3_selfcheck.jpg Self-Check

 

Do the following questions. When you are finished, check your answers.

 

SC 1. Measure the dimensions of your bedroom closet.

  1. What is its volume in cubic centimetres?
  2. What is its volume in cubic metres?
  3. Which unit of volume is more appropriate? Why?

SC 2. Measure the dimensions of a cereal box.

  1. What is its volume in cubic centimetres?
  2. What is its volume in cubic metres?
  3. Which unit of volume is more appropriate? Why?

SC 3. Convert 0.05 m3 to cubic centimetres.

 

SC 4. How much concrete, measured in cubic metres, is required for a driveway 3 m wide, 20 m long, and 15 cm thick?

 

Compare your answers.

 

Capacity

 

People use the word capacity in various ways. For example, the capacity of an elevator can refer to the number of passengers the elevator can safely hold. In SI, capacity refers to the amount of liquid a container can hold, or the amount of space inside the container.

 

“Capacity Animation” shows different ways of understanding the word. You will see that capacity is used in a special way when using SI for measurement.

 

capacity: a measurement of how much a container can hold

Commonly, capacity refers to the amount of liquid that can be poured into a container, but it can also be used to refer to an amount of solid that can be placed into a container.

In the Explore section, you placed sugar cubes in various rectangular, prism-shaped arrangements. You considered the dimensions of the boxes—imagined to be made of thin cardboard—that would hold the sugar cubes. You found that the dimensions of the boxes allowed you to calculate the volume of sugar the boxes could hold. That is, the product of the dimensions gave you the capacity of the boxes.

 

m10_3_trythis.jpg Try This

 

Look at various containers, such as soft-drink bottles, juice containers, and tinned goods. Record the metric measure of at least three containers. What SI unit is used?

 

litre: the capacity of a container having a volume of 1000 cm3

Since 1 L = 1000 mL, 1 mL = 1 cm3.

 

This drawing shows a 1-cm cube as having the capacity of 1 mL.

What does each of those SI symbols stand for?

 

What is the relationship between these units?

 

If you have a rectangular 1-L milk or juice container in the fridge, carefully measure its dimensions and calculate its volume. Round your answer to the nearest 1 cm3.

 

What is the relationship between the volume of the container and its 1-L capacity?

 

A container that has the shape of a cube measuring 10 cm (or 1 dm) on a side has a capacity of 1000 mL, or 1 L.

 

This drawing shows a 10-cm cube having a capacity of 1 L.

 

Here’s why.

 

 

 

 

 

 

 

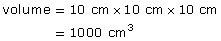
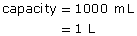
Why do you think a 1-L milk carton is not the shape of a cube having a side length of 10 cm?

 

Now you will practise applying these capacity units.

 

Example 3

 

On an Edmonton utility bill, the water a homeowner uses each month is reported in cubic metres.

 

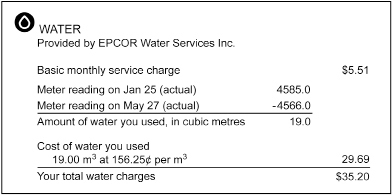
This graphic shows the back of an EPCOR bill listing a household’s water consumption.

Reproduced courtesy of EPCOR

 

This homeowner used 19 m3 of water last month. If this water was for a family of four, how many litres were consumed per person?

 

Solution

 

 

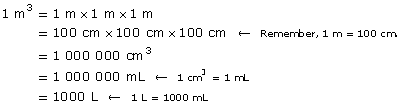
So, 19 m3 = 19 000 L.

 

Therefore, the consumption per person was

 

 

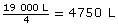
Example 4

 

Alexa has a small rectangular cooler she takes with her on picnics. The interior of the cooler is 32 cm long, 25 cm wide, and 25 cm deep. What is the capacity of the cooler in litres?

 

Solution

 

 

 

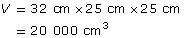
The cooler holds 20 L.

 

Units of Capacity

 

The prefixes of SI are used to form various units of capacity. You saw these prefixes when you investigated units of length, area, mass, and volume.

 

Prefix

Symbol

Factor

mega

M

1 000 000 or 106

kilo

k

1000 or 103

hecto

h

100 or 102

deca

da

10 or 101

—

—

1 or 100

deci

d

0.1 or 10–1

centi

c

0.01 or 10–2

milli

m

0.001 or 10–3

micro

µ

0.000 001 or 10–6

 

The following tables show how the units of capacity and volume compare. See how the relationship 1 cm3 = 1 mL in one row connect the two tables so that the amounts on corresponding rows are equivalent.

 

Capacity
Volume

Unit

Symbol

Symbol

Unit

1 millilitre

1 mL

1 cm3

1 cubic centimetre

1000 litres or
1 kilolitre

1000 L or 1 kL

1 m3

1 cubic metre

1 litre

1 L

1000 cm3 or 1 dm3

1000 cubic centimetres or 1 cubic decimetre

 

Move the sliders in “Capacity Conversions” to convert 1 kL into litres.

 

This will allow you to confirm the relationship between kilolitre and litre indicated in the capacity-volume table.

 

m10_3_selfcheck.jpg Self-Check

 

Now try these practice questions. To do these questions you will need to remember the relationships between volume and capacity. “Capacity Conversions” can be used to confirm your answers.

 

SC 5. A container of liquid laundry detergent holds 3.75 L. How many millilitres does this container hold?

 

SC 6. A soft-drink bottle holds 355 mL. How many litres does the container hold?

 

SC 7. Last month, the Ahenekiw family used 25 400 L of water in their home. How many cubic metres did they use?

 

SC 8. A rectangular aquarium is 50 cm long, 40 cm wide, and 30 cm deep. If it were filled with water, how many litres of water would the aquarium contain?

 

SC 9. When full, a rain barrel holds 220 L. What is the volume (in cubic metres) of the inside of the barrel?

 

SC 10. When full, a watering can holds 8 L. What is the volume of water it holds in cubic centimetres?

 

Compare your answers.

 

This photo shows Vancouver, British Columbia, with mountains and clouds in the background.

© Hannamariah/shutterstock

 

m10_3_mastcon.jpg Mastering Concepts

 

Try these questions. When you are finished, check your answers.

 

The area of Vancouver is almost 115 km2. On average, the city receives 1200 mm of precipitation each year.

 

MC 1. How many litres of water does this precipitation represent?

 

MC 2. There are seven billion people on Earth. If the water Vancouver receives as precipitation were divided equally, how many litres would each person receive. Round your answer to the nearest litre.

 

Compare your answers.

Answers will vary. Perhaps a 1-L milk carton is not this shape because other shapes are easier to hold in your hand, to pour, or to store on a shelf or in your refrigerator.
Answers will vary depending on the container’s shape. One such container sits on a square base with sides measuring 7 cm each and is 20.4 cm tall. Its volume is 7 cm × 7 cm × 20.4 cm = 999.6 cm3. Remember that 1 L = 1000 cm3.
1 L = 1000 mL
The unit L stands for litre, and mL stands for millilitre.
One SI (metric) symbol is mL. A soft-drink bottle might contain 300 mL, and a can of soup might hold 540 mL. Another symbol is L. A milk container might hold 2 L, or a large soft-drink bottle might hold 0.5 L.
Because there are 100 cm in a metre, a cubic metre is 100 cm × 100 cm × 100 cm, or 1 000 000 cm3.