Module 3
1. Module 3
1.9. Page 4
Module 3: Linear Measure
Bringing Ideas Together
Circles have been around for a long time. Just look at the architecture of historical buildings, such as the Taj Mahal and the Golden Temple.

© wong yu liang/shutterstock
This is the Taj Mahal.

© Ella/6375788/Fotolia
This is the Dome of the Rock.
Watch “Circles Are All Around Us,” which shows that circles remain important in the present and can be found in many modern settings. The multimedia piece also describes properties of circles, some of which you’ve already discovered in this lesson.
While watching, focus on the relationship between the diameter and circumference of a circle. Also try the interactive portion, which demonstrates the relationship between a circle’s diameter and circumference.
At the end of the interactive portion, the Greek letter ![]() (pi) is described. The value
(pi) is described. The value ![]() is given as 3.14. In the Explore section, you discovered that the ratio of the circumference of a circle to its diameter is always the same and is a bit larger than 3.
is given as 3.14. In the Explore section, you discovered that the ratio of the circumference of a circle to its diameter is always the same and is a bit larger than 3.
Because this ratio does not depend on the size of the circle, the value of this ratio can be represented by one symbol. Mathematicians also use the symbol because no decimal number can be used to represent the value exactly. The symbol represents the exact value of the ratio, ![]() .
.
If C = circumference and d = length of the diameter, then
![]()
The value of ![]() can be calculated to any number of decimal places.
can be calculated to any number of decimal places.
![]()
So, the value of ![]() is more than 3. It is close to 0.141 592 more than 3. See a very precise—but not exact—representation of 0.141 592 in the animation “A Circle Unrolled.” Select play in the animation.
is more than 3. It is close to 0.141 592 more than 3. See a very precise—but not exact—representation of 0.141 592 in the animation “A Circle Unrolled.” Select play in the animation.
The number for ![]() is a non-terminating, non-repeating decimal number. That means you cannot write a long-enough decimal representation to give its exact value. Fortunately, you do not have to memorize pi’s value, since there is a
is a non-terminating, non-repeating decimal number. That means you cannot write a long-enough decimal representation to give its exact value. Fortunately, you do not have to memorize pi’s value, since there is a ![]() key on your calculator!
key on your calculator!
The formula for ![]() has been added to the Formula Sheet. Download the “Formula Sheet” now and save it to your course folder. Like you do with the Glossary, every time you encounter a new formula, retrieve your copy of the Formula Sheet. If the formula is on the Formula Sheet, add notes or sketches to give the formula meaning to you. You can also add formulas to the Formula Sheet at any time.
has been added to the Formula Sheet. Download the “Formula Sheet” now and save it to your course folder. Like you do with the Glossary, every time you encounter a new formula, retrieve your copy of the Formula Sheet. If the formula is on the Formula Sheet, add notes or sketches to give the formula meaning to you. You can also add formulas to the Formula Sheet at any time.
You will use the Formula Sheet throughout the remainder of the course. Remember to save your changes to your course folder. Your Formula Sheet will be a great study tool.
Did You Know?
Some people put to the test their skill at memorizing digits of ![]() . In 2004, Daniel Tammet recited 22 514 digits of
. In 2004, Daniel Tammet recited 22 514 digits of ![]() . He did this without a mistake, and it took him over five hours to complete this task.
. He did this without a mistake, and it took him over five hours to complete this task.
Pi and the Formula for Circumference
Before you look at examples, review what you know about ![]() and its use in a formula for circumference. Watch “A Formula for Circumference.”
and its use in a formula for circumference. Watch “A Formula for Circumference.”
Example 1

© Pierdelune/shutterstock
The Temple of Hercules—near Rome, Italy—was built in the second century BCE. This temple has a diameter of 14.8 m.
- Estimate the temple’s circumference.
- Use your calculator to determine the circumference, correct to the nearest tenth of a metre.
- How can you tell if your answer to part b is reasonable?
Solution
- Circumference is about three times the diameter.
So, the circumference is approximately
3 × 15 m = 45 m
- You know, d = 14.8 m. You want to determine C.
Since the diameter was given, use
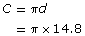
Enter the following keystrokes on your calculator.

If your calculator does not have a pi key, use 3.1416 for pi in your calculation.
3.1416 × 14.8 = 46.495 68
Round your answer to one decimal place (nearest tenth of a metre). You will find that you round up, since the second decimal in the product is a 9, regardless of whether you used the keystroke for pi or whether you entered the value for pi.
Therefore,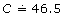 . Remember,
. Remember, 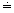 means “approximately equal to.”
means “approximately equal to.”
So, the circumference of the temple is approximately 46.5 m.
- The answer is reasonable, since the estimate in part a was 45 m.
Example 2
The diameter of the circular lid of an ice cream pail is 21 cm.
- Estimate the lid’s circumference.
- Use your calculator to determine the circumference, correct to the nearest tenth of a centimetre.
- How can you tell if your answer to part b is reasonable?
Solution
- Circumference is about three times the diameter.
So, the circumference is approximately
3 × 21 cm = 63 cm
- You know that d = 21 cm. You want to determine C.
Since the diameter was given, use
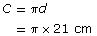
Enter the following keystrokes on your calculator.

Your display should be 65.973 445 . . ..
Round your answer to one decimal place (nearest tenth of a centimetre). You will find that you round up, since the second decimal in the product is 7.
Therefore,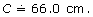
So, the circumference of the lid is approximately 66.0 cm.
- The answer 66.0 cm is reasonable since the estimate in part a was 63 cm.
Using Radius to Determine Circumference
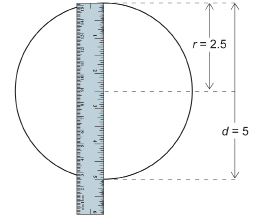
The circumference can also be found directly from the radius.
Remember that the diameter, d, of a circle is twice as long as its radius, r.
d = 2 × r or d = 2r
Once again, multiplication is understood and does not need to be shown in the formula.
If you combine the formulas for circumference and diameter, you will get the following.
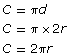
Examples 3 and 4 show how this formula can be applied.
Example 3
The radius of a bicycle wheel is 14 in.
- Estimate the circumference of the wheel.
- Calculate how far the wheel travels when it turns through one rotation. Express your answer in feet and inches. Round to the nearest inch.
- Is the answer to part b reasonable?
Solution
- Since r = 14 in, d = 2 × 14 in or 28 in.
So, the circumference is about 3 × 28 in, or 84 in.
- Since the radius was given, use
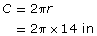
Enter the following keystrokes on your calculator.

Your display should be 87.964 594 . . ..
Round to the nearest decimal place. So, the circumference is about 88 in.
1 ft = 12 in, and 7 × 12 in = 84 in.
88 in = 7 × 12 in + 4 in, or 7 ft 4 in.
The wheel will travel 7 ft 4 in when it rotates once.
- The answer to part b is reasonable since the estimate in part a was 84 in.
 Self-Check
Self-Check
It is time to apply your skills! When you are finished, check your answers.
SC 1. The diameter of a circular element on an electric stove is 25 cm.
- What is the element’s radius?
- Estimate the circumference of the element.
- Calculate the circumference of the element to the nearest centimetre.
SC 2. The radius of a two-dollar coin is 14 mm. What is its circumference to the nearest millimetre?
Finding the Diameter and Radius from the Circumference
Suppose you were given the circumference of a circle, how would you find its diameter and radius?
The formula that involves circumference and diameter is ![]() To find the diameter, divide both sides of the equation by
To find the diameter, divide both sides of the equation by ![]() .
.
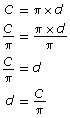
Example 4

© Carole Castelli/shutterstock
When a golf ball rolls on the green, it moves a distance of 13.5 cm each time it makes one rotation. What is the diameter of the ball, correct to the nearest tenth of a millimetre?
Solution
View the solution in “Example 4 Solution.”
 Self-Check
Self-Check
It’s time to check your skill! When you are finished, check your answers.
SC 3. The circumference of a baseball is 9.4 in. What is its diameter and radius to the nearest tenth of an inch?
SC 4. Without using your calculator, estimate the diameter of a circular cake pan with a circumference of 27 in.
 Mastering Concepts
Mastering Concepts
Try this question. When you are finished, check your answer.
A golfer is about to putt 12 ft 4 in from the cup. How many times must his ball rotate to reach the hole? The diameter of the golf ball is 1.68 in.