Module 3
1. Module 3
1.12. Page 2
Module 3: Linear Measure
Get Started
In the following Try This activity, you will investigate one method for finding the middle of a rectangular object.
Try This
At first you may find it a challenge to accurately identify the middle of an object. Try marking the middle of some objects presented in the interactive activity, “Find the Middle.”
From your experience with “Find the Middle,” it’s clear that a guess-and-check approach does not always get you to the middle.
The following approaches are both more methodical and more reliable. Work with a partner if possible.
Folding to Find the Midpoint
Step 1: Take a blank sheet of standard paper, like those commonly used in computer printers (8.5 in × 11 in). Fold the sheet of paper in half from top to bottom.
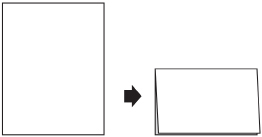
Step 2: Then fold the paper in half again, this time from left to right.
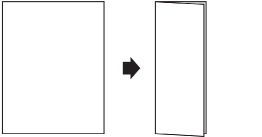
Step 3: When you open the folded sheet, the creases will pass through the centre of the sheet.
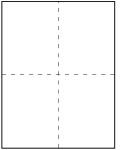
This method worked to find the centre of the sheet of paper. But what if you were trying to find the centre of a rectangular wood board? Folding wood to find the middle would not be an option. How could you find the middle of the wood board? Here is one possibility.
Using the Diagonal to Find the Midpoint
Non-adjacent vertices are vertices that are not end points of the same side. For example, a diagonal of a rectangle is a line joining opposite corners.
Step 1: Pretend your sheet of paper is a wood board. Lay a ruler or straight edge from one corner of the sheet to the opposite corner. Use your pen to draw this diagonal. What do you notice?
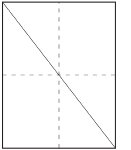
Step 2: Use your straight edge to draw in the second diagonal.
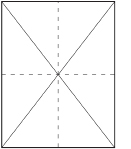
The diagonals of the rectangle cross each other where the creases meet. This is the middle point of the sheet of paper (or of your imaginary wood board).
vertical: perpendicular to the level of the ground
On a sheet of paper, the vertical direction is parallel to the left and right sides of the paper.
horizontal: parallel to the level of the ground
On a sheet of paper, the horizontal direction is parallel to the top and bottom sides of the paper.
midpoint: the point at the middle or centre of an object
Step 3: How far is the midpoint of the sheet from the edges of the sheet? Use your ruler or tape measure to check these distances. Remember to measure the distances along the vertical and horizontal creases.
You have just discovered two ways to find the middle of a rectangular object. This middle point is also referred to as the midpoint.
Place your sheet with folds, diagonals, and notes about finding the centre of a rectangle in your course folder.
In the calculation to measure the distances from the midpoint to the edges of the sheet, you may have noticed it can be inconvenient to work with decimals and inches—especially if you are using a tape measure and working with lumber.
When speaking about lumber, a 1 × 6 is actually a board that is just 
in × 
in. The 1 × 6 gets its name from its dimensions before it is made smaller through drying and planing. How would you divide the finished dimension of this board (
in × 
in) by 2?
Sometimes being able to calculate with fractions is easier than calculating with decimals. So, before going further, you will review dividing fractions.
Example 1
What is 
?
Solution
Method 1
View “Example 1 Solution.”
Method 2
You could use your calculator to solve the equation, since you likely know the decimal equivalent of the fraction 
is 0.75.
So,
Example 2
Find 
Solution
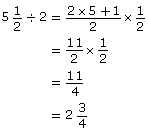
Check using your calculator.
Self-Check
The following questions could be encountered in carpentry, sewing, or in many other occupations. Check your answers using a calculator. If you are working with a partner, take turns dividing the fractions and using the calculator.
SC 1.
SC 2.
SC 3.
SC 4.
11 ÷ 2. From the sides of the sheet, the centre should be 4.25 in, which is 8.5 in ÷ 2. (Note that
4.25 in =
in.).