Module 4
1. Module 4
1.8. Page 3
Module 4: Area
Explore 1
Now that you have reviewed some characteristics of polygons, you may be wondering about the area of these shapes. For example, you may be curious about the area of a parallelogram. Well, that is the topic of the next activity.
 Try This
Try This
Watch the animation “Area Relationship,” or use the following three steps to explore the relationship between the area of a parallelogram and the area of a rectangle with similar dimensions.
Step 1: Print one copy of Parallelogram.
Step 2: Cut out the parallelogram.
Step 3: Cut along the dashed line segment representing the height. Move the triangle that was on the left to the right. Fit the cut-out triangle with the rest of the shape to form a rectangle.
Based on what you saw from the “Area Relationship” animation or from the steps above, complete these questions.
TT 1.
- What was the length of the base of the original parallelogram?
- What was the height of the original parallelogram?
TT 2.
- What is the length of the rectangle?
- What is the width of the rectangle?
- How do these values compare to the base and height of the original parallelogram?
TT 3.
- What is the area of this rectangle?
- How does this area compare to the area of the original parallelogram?
Place a copy of your answers in your course folder.
 Try This
Try This
Use “Demonstration Applet: Perimeter and Area (Parallelogram)” to explore how the area of a parallelogram relates to its dimensions. Notice the following about this multimedia piece.
- The variable m is used for the base of the parallelogram.
- The variable h is used for the height.
- You should not use the slider under n.
- The perimeter of the parallelogram is given (which you can ignore).
Use the applet to create the same parallelogram you explored in the previous Try This activity (TT 1 to TT 3). The area calculated by the applet should match the area of the parallelogram you calculated in TT 1 to TT 3. Did yours match? You will notice that slant height/length is a variable in the applet that you do not use in the area calculation.
TT4. When would slant length/height be useful?
Place a copy of your answer in your course folder.
Areas of a Parallelogram and a Rectangle Compared
In the previous activities you showed that the area of a parallelogram is the area of a rectangle with the same base and height. In other words, area of parallelogram = base × height, or A = bh.
You discovered a way to find the area of a parallelogram by rearranging the parallelogram’s area to make another figure. Rearrangement of areas can be used to gain insight into the area of a triangle as well.
 Try This
Try This
In this activity you will explore the area of a triangle.
Step 1: On a sheet of grid paper, draw two identical triangles; or print and use Pair of Triangles. A sample is shown below.
TT 5.
- What is the length of the base of each triangle?
- What is the height of each triangle?
Step 2: Cut out both triangles. Arrange the triangles to form a parallelogram with the same base length as the base of each triangle.
TT 6.
- What is the length of the base of the parallelogram?
- What is the height of the parallelogram?
TT 7.
- What is the area of the parallelogram?
- What is the area of each triangle?
 Share 1
Share 1
Share your answers to TT 7 with a partner or group. How did the areas of the parallelograms and triangles compare? What relationship can you see between these areas? How is this relationship shown in the formulas used to calculate the area of a parallelogram and the area of a triangle?
Write a paragraph that answers these Share questions. Use example values from your discussion partners in your explanation.
Place this paragraph in your course folder for future reference.
Area of a Triangle
In the Try This activity you just completed (TT 5 to TT 7), you may have noticed that the area of a triangle is half the area of a parallelogram with the same base and height. This idea can be expressed this way.
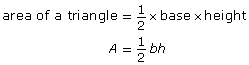
 Try This
Try This
Use the applet “Area of a Triangle” to explore the area of triangles and the formula ![]() .
.
Note that, in the applet, altitude = height. When you use the applet, include triangles with all of the following shapes.