Module 4
1. Module 4
1.10. Page 5
Module 4: Area
Explore 2
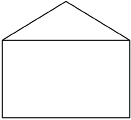
Composite Shapes
Often, more complicated figures are formed by combining simpler geometric shapes.
For instance, the end of a garage looks like a triangle on top of a rectangle. This more complicated shape can be considered to be a composite figure.
Combining simpler shapes, such as the triangle, rectangle, parallelogram, and circle, results in a composite figure.
In the next activity you will investigate the area of a trapezoid.
composite figure: any shape formed by combining simpler shapes
trapezoid: a quadrilateral with one pair of parallel sides
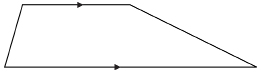
In this trapezoid, the pair of sides that are parallel are marked by arrows.
 Try This
Try This
If possible, work with a partner.
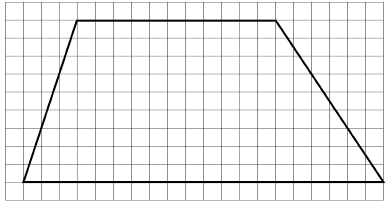
In this activity you will investigate the shape of a trapezoid and how aspects of its shape can help you determine its area.
Save your work from this Try This activity and Share 2, which you will complete in a few moments. You will be prompted to include this communication in your Lesson 2 Assignment soon.
Draw a trapezoid on a sheet of Quarter-Inch Grid. Draw a trapezoid on the grid paper. If you are working with a partner, draw different trapezoids.
In Get Started you reviewed finding areas of parallelograms and triangles. You were introduced to the concept that many objects are composites, containing objects of many different shapes.
TT 8. Identify different-shaped objects that are combined to form the trapezoid above. Sketch these shapes within the diagram.
TT 9. Come up with a strategy you would use to calculate the area of the trapezoid using the areas of the component shapes you have identified.
 Share 2
Share 2
Share your work from TT 8 and TT 9 with other students. You will probably see many different approaches from the one you developed. Evaluate each of the strategies.
- Have they identified appropriate shapes within the trapezoid?
- Do the formulas they used in TT 9 make sense?
- Which approach has the fewest shapes within the trapezoid?
Make a list of aspects that make certain approaches more effective in your opinion. Summarize what you have discussed in this Share by answering the following questions and saving them in your course folder.
- Which approach seems to be the most effective at calculating the area of the trapezoid?
- Calculate the area for the trapezoid using a minimum of two of the approaches you have seen. Do you get the same answer with each approach?
- Which approach will you use in the future? Why?
Save a copy of your discussion in your course folder. Include a copy of your work from the Share 2 section in Part 1 of your Lesson 2 Assignment document.
Splitting the Trapezoid
Were you surprised by the number of approaches of calculating the area of the trapezoid in the previous activity? Did one of the approaches identify only two component shapes? If not, you might find the approach you will see in the following Self-Check helpful for your future work.
 Self-Check
Self-Check
Draw a trapezoid without using a grid. Call the height h and the lengths of the two parallel sides a and b.
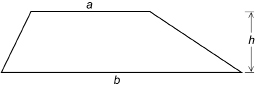
Then divide the trapezoid into two triangles.
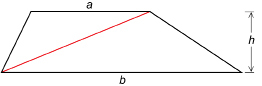
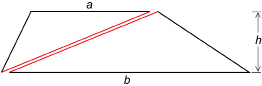
SC 4. The upper triangle has a base length of a units long and a height of h units. What is the area of the upper triangle?
SC 5. The lower triangle has a base of b units and a height of h units. What is the area of the lower triangle?
SC 6. What is an expression for the area of the trapezoid?
If you did not identify the trapezoid as containing two triangles, redo the previous Try This activity (TT 8 and TT 9) to see if this approach allows you to calculate the area of a trapezoid.