1. Module 4

1.16. Page 4

Mathematics 10-3 Module 4 Lesson 3

Module 4: Area

 

Bringing Ideas Together

 

In the Explore you discovered that the area of a circle is approximately the area of a parallelogram formed by fitting wedges or sectors of the circle together. This procedure can be used to develop the formula for the area of a circle in terms of its radius.

 

The formula for the area of a circle was obtained from the parallelogram with a base of eqn212.eps.

 

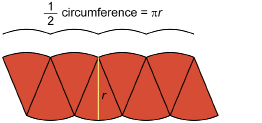
This illustration shows a circle cut into 8 parts and the parts positioned to form an approximation to a parallelogram.

 

This is one-half the circumference of the original circle, because half of the sectors of the circle are across the top and half are across the base.

 

 

eqn062.eps

 

The height of the parallelogram is the radius of the circle, r. So,

 

 

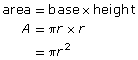
eqn063.eps

 

Now study the examples that follow, which use the area of a circle formula. You will see that this formula works with SI and imperial units.

 

Example 1

 

This photograph shows a maintenance-hole cover and a man working over the uncovered space.

© Lynne Furrer/shutterstock

The diameter of a circular steel maintenance-hole cover is 24 in. What is its area in square feet? Round your answer to two decimal places.

 

Solution

 

1 ft = 12 in

 

eqn064.eps

 

diameter = 2 ft

 

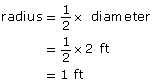
eqn065.eps

 

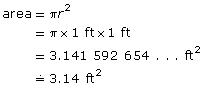
eqn066.eps

 

The area of the maintenance-hole cover is about 3.14 ft2. This is about three times the square of the radius.

 

Did You Know?

 

Maintenance-hole covers are made round so that they cannot slip down into the hole. A square, rectangular, or oval cover could fall into the hole. Can you think of why it is important that the cover not fall into the hole?


 

Example 2

 

This photograph shows a circular punch bowl.

© Edgewater Media/shutterstock

A circular punch bowl has a radius of 15 cm. If the bowl is filled to the brim, what area of the punch is exposed to the air? Round to the nearest square centimetre.

 

Solution

 

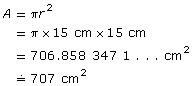
eqn067.eps

 

Approximately 707 cm2 of punch is exposed to the air.

 

Now practise your skills.

 

m10_3_selfcheck.jpg Self-Check

 

Answer the following questions. When you are finished, check your answers.

 

This photograph shows a lawn sprinkler rotating as it sprays water.

© Eva Blanda/shutterstock

SC 6. A circular cookie cutter has a diameter of 3 in. What is the area of dough this cookie cutter will cut? Round to one decimal place.

 

SC 7. A water sprinkler covers a circular area 12 ft in radius. What area does the water cover? Round to the nearest square foot?

 

SC 8. If you did not have a calculator, how might you estimate the area the sprinkler covered in SC 7?

 

Compare your answers.

 

Composite Figures

 

In Lesson 2 you investigated areas of composite figures. In this lesson you will explore composite figures involving circles. Use the applet “Exploring Composite Figures” to form the composite shape used in Example 3 that follows. The applet will show the formulas needed to calculate the area of each shape in the composite figure. This can be a helpful place to start when solving composite figure problems.

 

Example 3

 

The following is a plan for a backyard ice rink. The ends of the rink are semicircles.

 

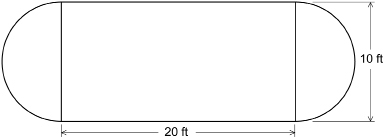
This illustration shows a backyard skating rink. It is composed of a rectangular length of 20 feet by a width of 10 feet with semicircular ends with a diameter of 10 feet.

 

What is the area of the rink to the nearest square foot?

 

Solution

 

To find the area of the rink, you can separate the rink into a circle and a rectangle.

 

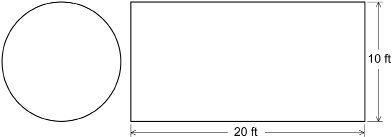
This illustration shows the backyard skating rink broken into its components. There is a circle with a radius of 10 feet and a rectangle 10 feet by 20 feet.

 

Find the area of the circle. The circle’s diameter is 10 ft, so the radius is 5 ft.

 

 

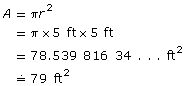
eqn073.eps

 

Find the area of the rectangle.

 

 

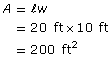
eqn074.eps

 

 

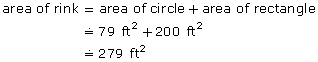
eqn075.eps

 

The area of the rink is approximately 279 ft2.

 

The Breakdown

 

As in the Example 3, the steps in finding areas of composite figures are as follows.

 

Step 1: Break the figure into simple shapes.

 

Step 2: Transfer the dimensions to the simple shapes.

 

Step 3: Find the area of each simple shape.

 

Step 4: Combine the areas. Sometimes you will add areas, and sometimes you will subtract areas.

 

m10_3_selfcheck.jpg Self-Check

 

Answer the following questions. When you are finished, check your answers.

 

You may find the applet “Exploring Composite Figures” helpful if you are stuck on a question.

 

SC 9. Bernie is preparing a costume for a party. She has cut a circle 16 cm in diameter out of a trapezoidal piece of cloth.

 

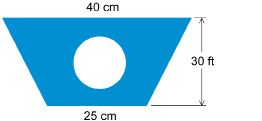
This illustration shows a trapezoid with a height of 30 centimetres and parallel bases of 25 centimetres and 40 centimetres. The trapezoid has a circular hole in the middle with a diameter of 16 centimetres.

 

Determine the area of the remaining cloth. Round to the nearest square centimetre.

 

What two simple shapes are there in this composite figure?

 

SC 10. The following is a side panel for a toy car. The wheels have a diameter of 6 in each. What is the area of the coloured panel? Round to the nearest square inch.

 

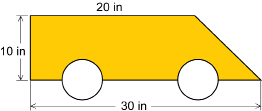
This illustration shows a coloured trapezoidal toy car. The coloured trapezoid is 10 inches high with parallel bases of 30 inches and 20 inches. There are two 6-inch diameter wheels with half of each wheel cut out from the coloured trapezoid.

 

Compare your answers.

 

m10_3_mastcon.jpg Mastering Concepts

 

Try these questions. When you are finished, check your answers.

 

MC 1. What is the area, to the nearest square inch, of the largest circle that can be cut from a square floor tile that measures 1 ft2 in area?

 

MC 2. What area of the tile is waste?

 

Compare your answers.