Module 4

Module 4: Area

 

Bringing Ideas Together

 

In Explore you found the surface area of a conical cup. Now you will study the conical cup’s net to develop the formula for the surface area of any cone.

 

 

 

 

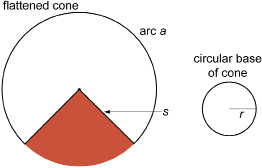
circumference of circular base, which completes the arc, is

 

 

So, as in Explore,

 

 

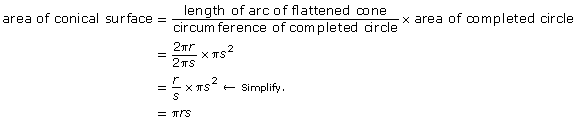
surface area of cone = area of conical surface + area of circular base

 

 

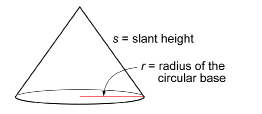
Remember, r is the radius of the base of the cone, and s is the slant height measured along the surface of the cone.

 

Take a look at “Exploring Surface Area, Volume, and Nets.” Use this applet to compare the surface area formula for a cylinder with that of a cone. You can use this to check your work as you go through the practice questions.

 

Now, you will practise using the formulas for the surface area of a cylinder and a cone. You will need a calculator.

 

Example 1

 

The cost of aluminum in a soup can depends on the can’s surface area. A cylindrical soup can is 6.5 cm in diameter and 9.5 cm high. What is its surface area? Round to one decimal place.

 

Solution

 

First, determine the radius.

 

 

Now you’re ready to calculate surface area.

 

 

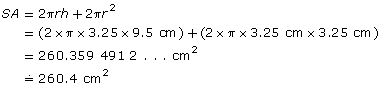
The surface area is approximately 260.4 cm2.

 

Example 2

 

How could you estimate the surface area of the soup can in Example 1 to check whether the answer is reasonable?

 

Solution

 

Since you could first round the value of to 3.

 

So, 2 is about 6.

 

Therefore, surface area of the cylinder is about 6rh + 6r2.

 

Also, you could round the radius 3.25 cm to 3 cm and the height 9.5 cm to 10 cm.

 

So,

 

 

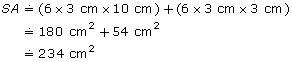
This is close to the calculated answer, 260.4 cm2. The answer in Example 1 is reasonable.

 

Example 3

 

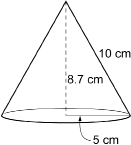
Determine the surface area of the following cone. Round to the nearest square centimetre.

 

 

Solution

 

r = 5 cm

 

s = 10 cm (Note that s is the slant height. Do not use 8.7 cm, which is not the slant height.)

 

 

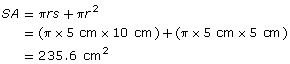
Once again, you could approximate the surface area by using 3 as a value of .

 

 

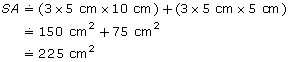
The surface area of the cone is 235.6 cm2. The answer is reasonable, as it is close to the estimate of 225 cm2.

 

Now it’s your turn. The following Self-Check questions can be solved in a similar manner to the examples you have just studied.

 

Self-Check

 

Answer the following questions. When you are finished, check your answers.

 

SC 2. During harvest on the Prairies, you will often see wheat stored in conical piles in the fields. The wheat is protected from soil moisture by a plastic ground sheet. A conical pile of wheat 15 ft in diameter will be about 3.5 ft high and have a slant height of about 8.3 ft. What is the surface area of the pile exposed to the air? Round to one decimal place.

 

 

SC 3. Jeremy is hired to paint a cylindrical silo that is 65 ft high and 20 ft in diameter. To buy enough paint, Jeremy must calculate the surface area of the silo. What is the area of the top and cylindrical side of the silo? Round to the nearest 100 ft2.

 

SC 4. A cylindrical fuel tank on Bev’s farm is 6 ft long and 4 ft in diameter. What is the total surface area of the tank? Round to the nearest square foot.

 

SC 5. This picture shows a view of a seed-cleaning plant in Alberta. The hoppers are shaped in the form of a cylinder on top of a cone. If the diameter of the cylinder is 12 ft, the height of the cylindrical portion is 18 ft, and the slant height of the cone is 8 ft, what is the area of the outside of the cylinder and cone? Round to the nearest square foot.

 

Compare your answers.

 

Mastering Concepts

 

Try this question. When you are finished, check your answer.

 

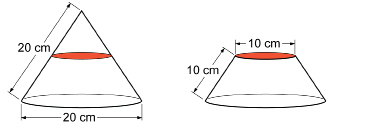
A wooden cone with a diameter of 20 cm and a slant height of 20 cm is cut halfway up into two pieces. The top is discarded. What is the surface area of the remaining bottom piece shown on the right (including the newly flattened top)? Round your answer to the nearest square centimetre.

 

 

Compare your answers.

 

Mathematics 10-3 Learn EveryWare © 2010 Alberta Education