1. Module 4

1.30. Page 3

Mathematics 10-3 Module 4 Lesson 6

Module 4: Area

 

Explore

 

In this Try This activity you will explore how the perimeter and the area of a rectangle change when the dimensions of the rectangle change.

 

Try This

 

Step 1: Make a rectangle that has sides of 1 unit wide by 2 units long (1 × 2). You will need Quarter-Inch Grid, or you may use the demonstration applet “Perimeter and Area (Rectangle)” again.

 

Step 2: Calculate and record the perimeter and area for each rectangle. Then record the measurements in the table “Perimeter and Area of Rectangles,” also shown in Step 6. Remember to save your table in your course folder.

 

Step 3: Make another rectangle. To obtain the dimensions of the second rectangle, multiply the dimensions of the first rectangle, shown in red, by 2. So, for the second rectangle, the length will be 2 × 2 = 4, and the width will be 2 × 1 = 2.

 

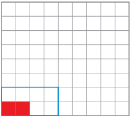
This illustration shows a 2 by 1 red rectangle in the lower left corner of an outlined 4 by 2 blue rectangle. Both rectangles are on grid paper.

 

The original rectangle is drawn in red, and the rectangle for a scale factor of 2 is shown outlined in blue.

 

scale factor: a number used to multiply the dimensions of a 2-D shape, such as a rectangle

Step 4: Make a third rectangle. To obtain the dimensions of the third rectangle, multiply the dimensions of the first rectangle, shown in red, by 3. So, for the third rectangle, the length will be 3 × 2 = 6, and the width will be 3 × 1 = 3.

 

The numbers by which you multiply the dimensions of the original rectangle are called scale factors.

 

Step 5: Draw the rectangles for scale factors 4, 5, and 6. Each additional rectangle you draw will be similar in shape; that is, each rectangle will be twice as long as it is wide.

 

Step 6: Complete the table, and then use the table to answer the following Try This questions. The first two rows are completed for you.

 

Perimeter and Area of Rectangles

 

1

2

3

4

5

6

Scale Factor

Dimensions of Rectangle

Perimeter in Units

perimeter of rectangle

perimeter of original rectangle

Area of Rectangle in Units2

area of rectangle

area of original rectangle

1

= 2

w = 1

6

2

2

= 4

w = 2

12

8

3

 

 

 

 

 

4

 

 

 

 

 

5

 

 

 

 

 

6

 

 

 

 

 

 

TT 7. What happens to the perimeter when the scale factor is increased by 1?

 

TT 8. If the scale factor were 7, how many times greater would the perimeter of the new rectangle be compared to the perimeter of the original rectangle?

 

TT 9. If the scale factor were 7, how many times larger would the area of the new rectangle be compared to the area of the original rectangle?

 

TT 10. If the scale factor were k, how many times longer would the perimeter of the new rectangle be compared to the perimeter of the original rectangle?

 

TT 11. If the scale factor were k, how many times larger would the area of the new rectangle be compared to the area of the original rectangle?

 

Share

 

Discuss the following questions with a partner or in a group. The questions are based on the charts you completed in the Try This parts of this lesson.

  • Do you see a relationship between the numbers in column 1 and column 4 of the charts? If there is a relationship, what is that relationship?
  • Do you see a relationship between the numbers in column 1 and column 6 of the charts? If there is a relationship, what is that relationship?
  • Suppose both dimensions of a rectangle are doubled, which is affected more—the perimeter or the area?

Summarize your discussion and place a copy in your course folder.