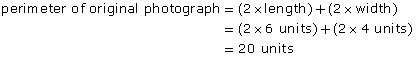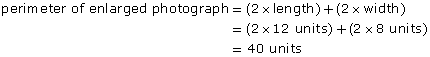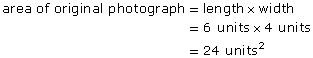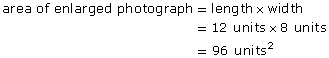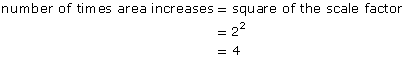1. Module 4

1.31. Page 4

Mathematics 10-3 Module 4 Lesson 6

Module 4: Area

 

Bringing Ideas Together

 

In Getting Started, Explore, and Share you discovered the following:

  • If both the length and width of a square or rectangle are changed, then the perimeter and area change.
  • If the scale factor for changing a figure is k, the perimeter of the new figure is k times the perimeter of the original figure.
  • If the scale factor for changing a figure is k, the area is k2 times the area of the original figure.

Study the following examples.

 

This is an image of the flag of British Columbia shown in two sizes. The original is on the left and is smaller than the enlarged version on the right. The flags are on a grid. The left flag covers a 4-by-6 area of the grid. The right flag covers an 8-by-12 area of the grid.

© Jiri Flogel/shutterstock

Example 1

 

The photograph of the British Columbia flag on the right has been enlarged.

 

Part 1

  1. By what scale factor has the small flag been enlarged?
  2. What is the perimeter, in units, of the original image of the flag?

  3. What is the perimeter of the enlargement?

  4. How many times longer is the perimeter of the enlargement than the perimeter of the original photograph?

  5. How does the scale factor predict the change in perimeter?

Solution

  1. The length of the enlargement is 12 units. The length of the original photograph is 6 units.

     

     



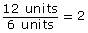
    The width of the enlargement is 8 units. The width of the original photograph is 4 units.

     

     



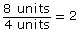
    Both the length and width were increased 2 times. The scale factor is 2.


  1. perimeter of enlargement = 2 × perimeter of original

    The perimeter of the enlargement is 2 times the perimeter of the original.
  1. The number of times the perimeter increases is equal to the scale factor.

Part 2

  1. What is the area, in square units, of the original photograph?
  2. What is the area of the enlargement?
  3. How many times larger is the area of the enlargement than the area of the original photograph?
  4. How does the scale factor predict the change in area?

Solution



Example 2

 

The square window in Jerritt’s bathroom is times as long on each side as his bedroom window.

 

This is a photograph of a bathroom with a small window.

© David Hughes/shutterstock

This is a photograph of a bedroom with a larger window.

© Joseph Calev/shutterstock



  1. How much shorter is the trim on the bathroom window than the same trim on the bedroom window?

  2. The amount of light a window lets in depends on its area. How many times less light does the bathroom window let in than the bedroom window?

Solution

  1. The scale factor is .

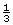    perimeter of Jerritt’s bathroom window =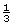 × perimeter of bedroom window

    Jerritt’s bathroom window has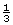 times the length of trim of the bedroom window.

  2. The scale factor is .

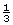    area of Jerritt’s bathroom window = ×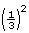 area of bedroom window

    Jerritt’s bathroom window lets in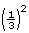 , or 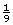, times as much light as the bedroom window.

Example 3

 

Two rectangular blankets are the same shape but different sizes. The perimeter of the larger blanket is 4 times the perimeter of the smaller blanket. How many times is the area of the larger blanket than the smaller?

 

Solution

 

The scale factor is 4.

 

 

The area of the larger blanket is 16 times the area of the smaller blanket.

 

Example 4

 

The area of a square mirror is 25 times the area of a smaller square mirror. How many times longer is each side of the larger square mirror than the smaller?

 

Solution

 

number of times area changes = (scale factor)2

 

Since 25 = 52, the scale factor is 5.

 

The sides of the larger mirror are 5 times as long as the sides of the smaller mirror.

 

This graphic shows an original image and a black-and-white photocopy of the same image. The area of the photocopy is one-quarter of the area of the original.

© Tischenko Irina/shutterstock

Example 5

 

The area of a photocopied image of sunflowers has an area the area of the original. How many times shorter is each side of the photocopied image compared to the corresponding side in the original?

 

Solution

 

number of times the area changes = (scale factor)2

 

Since , the scale factor is .

 

Each side of the photocopied image is of the length of the corresponding side in the original.

 

Self-Check

 

There are many practical applications involving changes in scale. Answer the following questions to apply these skills. When you are finished, check your answers.

 

A photo shows a llama.

© Dreef/4191313/Fotolia

SC 1. Janice is planning a rectangular enclosure for her llamas. She can only afford 100 m of fencing. How many times larger in area would a similarly shaped enclosure be if she could afford 300 m of fencing?

 

SC 2. Dakota has two square cake tins. One tin is 8 in on a side. The other tin is 12 in on a side. If Dakota bakes a cake in each tin, how many times larger is the area of the top of the larger cake than the smaller cake?

 

SC 3. Sigrid has used a photo enlarger at her school to double the area of a class photo.

  1. What is the scale factor? Round your answer to three decimal places.
  1. If the dimensions of the original photo were 5 in by 7 in, what are the dimensions of the enlargement? Round to the nearest inch.

SC 4. Renée is interested in model aircraft. She is building a model of the Harvard Trainer that was used to train Canadian pilots in World War II. If the length of the Harvard were 29 ft 6 in, how long will Renée’s model be to the nearest inch?

 

SC 5. A square that measures mile on a side contains 160 ac. How many acres would there be in a square that measures 2 mi on a side?

 

SC 6. The dimensions of a rectangular deck are increased by a factor of 2.5. The original perimeter of the deck was 30 ft. What is the perimeter of the enlarged deck?

 

This photograph shows a deck.

Hemera/Thinkstock

 

SC 7. How many times was the area of the deck in SC 6 increased?

 

Compare your answers.

 

Irregular Changes to Squares and Rectangles

 

The examples and the Self-Check questions dealt with squares and rectangles for which both dimensions were increased by a given scale factor. If both length and width are not increased by the same factor, it is best to solve each problem without using a formula involving a scale factor.

 

Example 6

 

This illustration shows two rectangles. The rectangle on the left measures 10 centimetres by 4 centimetres. The rectangle on the right measures 30 centimetres by 4 centimetres. The right rectangle is divided into 3 smaller equal rectangles.

A rectangle measures 10 cm by 4 cm. A second rectangle measures 30 cm by 4 cm.

 

Compare the perimeters and areas of the two figures.

 

Solution

 

The length of the second rectangle is 3 times the length of the first rectangle. The widths are the same.

 

Step 1: Compare the areas.

 

From the diagram, the area of the second rectangle appears to be 3 times the area of the first rectangle.

 

Check the following:

 

 

 

Since, 3 × 40 cm2 = 120 cm2, the second rectangle is 3 times the area of the first.

 

Step 2: Compare the perimeters.

 

 

 

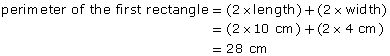
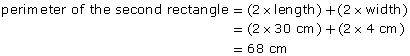
The perimeter of the second rectangle is not 3 times the perimeter of the first rectangle. Three times the perimeter of the first rectangle would be 84 cm. The second rectangle’s perimeter is only 68 cm.

 

Example 7

 

A rectangle is 3 cm wide and 5 cm long. If it were made twice as wide and 3 times as long, how would the area and perimeter change?

 

Solution

 

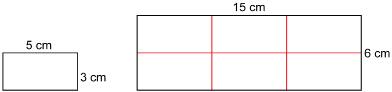
This illustration shows two rectangles. The left rectangle measures 5 centimetres by 3 centimetres. The right rectangle measures 15 centimetres by 6 centimetres. The right rectangle is divided into six smaller equal rectangles.

 

The new rectangle is 3 × 5 cm = 15 cm long and 2 × 3 cm = 6 cm wide.

 

Step 1: Compare the areas.

 

From the diagram, it appears that the new rectangle is 3 × 2, or 6, times the area of the original rectangle.

 

Check the following:

 

 

 

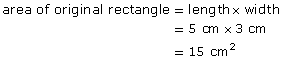
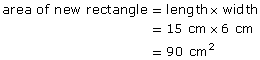
Since 6 × 15 cm2 = 90 cm2, the area was increased 3 × 2, or 6, times.

 

Step 2: Compare the perimeters.

 

 

 

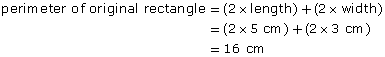
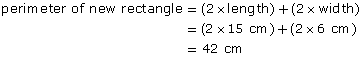
Notice that the perimeter is not 2 times, or 3 times, or even 6 times the perimeter of the original figure. You have to determine the perimeters from the dimensions of each rectangle. There is no shortcut for perimeter.

 

Factors Affecting Area

 

From the previous two examples, notice that if the length of a rectangle is increased m times and its width is increased n times, the area increases m × n times. This formula applies to area only.

 

Self-Check

 

Answer the following questions. When you are finished, check your answers.

 

SC 8. The length of a certain rectangle is changed by a factor of 5 and its width by a factor of 2. If the area of the original rectangle were 23 ft2, what is the area of the new rectangle?

 

SC 9. The width of a square is enlarged 7 times. The length is increased by a factor of 9. How many of the original squares would fit into the new figure? Include a diagram in your solution.

 

Compare your answers.

 

Mastering Concepts

 

Try these questions. When you are finished, check your answers.

 

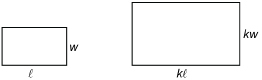
This illustration shows two rectangles. The left rectangle has dimensions l and w. The right rectangle has dimensions kl and kw.

MC 1. Show that if both the length and width of a rectangle are scaled by a factor of k, the area of the new rectangle is k2 times the area of the original, and the new perimeter is k times the original perimeter.

 

MC 2. A rectangle is enlarged to give an area that is twice the original area. What changes to the length and/or width could have caused the doubling of area?

 

Compare your answers.