1. Module 5

1.4. Page 4

Mathematics 10-3 Module 5 Lesson 1

Module 5: Angles

 

Bringing Ideas Together


right angle: one-quarter of a complete rotation

 

It is 90° in measure.

 

acute angle: an angle greater than 0° but less than 90°

This is an acute angle.

 

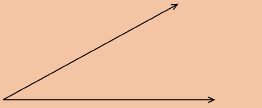
This is an illustration of an acute angle that opens to the right.

 

obtuse angle: an angle greater than 90° but less than 180°

This is an obtuse angle.

 

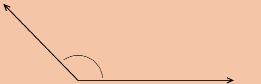
This is an illustration of an obtuse angle that opens to the right.

 

straight angle: one-half of a rotation; an angle of 180°

This is a straight angle.

 

This is an illustration of a straight angle.

 

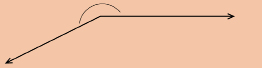
reflex angle: an angle having a measure greater than 180° but less than 360°

This is a reflex angle.

 

This is an illustration of a reflex angle.

 

full rotation: an angle having a measure of 360°

This is a full rotation angle.

 

This illustration shows a full rotation angle.

In Getting Started and Explore, you reviewed the parts of an angle, how they are measured, and what referents may be used to estimate their size. Before adding to your estimation skills, you will revisit how angles are classified by measure.

 

In Explore, you began by folding a sheet of paper to divide one complete rotation into quarters.

 

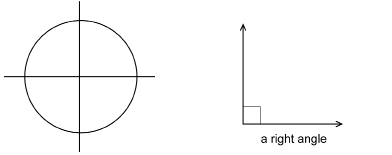
The left illustration shows a circle divided into four equal quadrants by a horizontal and a vertical line, and the right illustration is of a right angle.

 

Each of the four angles was in measure.

 

Most home designs involve countless right angles. Walls and floors meet at right angles—corners are square. A small square is often drawn between the arms of a right angle.

 

Use the applet “Acute Angle” to investigate acute angles. As you drag the movable dot to change the angle size, watch for a colour change in the text. Between what degrees is an angle considered acute? What happens if the angle is greater than 90°?

 

The word acute means “sharp.” Do you agree this is an appropriate name to describe what you now know as acute angles?

 

Use the applet “Obtuse Angle” to investigate obtuse angles. Between what degrees is an angle considered obtuse?

 

You should now be able to define the term obtuse angle.

 

Did You Know?

 

The word obtuse means “dull.”

 

 

 

 

 

Use the applet “Straight Angle” to investigate straight angles, which are a type of angle that can look like a simple straight line.

 

Another type of angle is a reflex angle. Use the applet “Reflex Angle” to investigate this type of angle.

 

Estimating Angle Measures with Referents

 

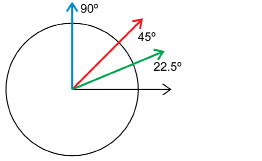
The illustration shows a circle with angles marked at 22.5 degrees in green, 45 degrees in red, and 90 degrees in blue.

Next, you will estimate angles using the referents you discovered in Explore. You will need the circle diagram you prepared through paper folding and the triangle containing the 30° and 60° angles.

 

Look at your circle diagram again.

 

The 45° angle (red) is .

 

The 22.5° angle (green) is .

 

If you were to place 30° and 60° on the circle, those angles would divide the right angle into three parts.

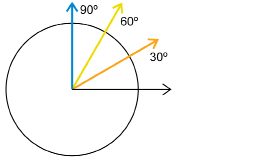
The illustration shows a circle with angles marked at 30 degrees in orange, 60 degrees in yellow, and 90 degrees in blue.

 

The 30° angle (orange) .

 

The 60° angle (yellow) .

 

So, 30°, 60°, and 90° are also useful benchmarks or referents.

 

Study the following examples to hone your estimation skills. You will be working with acute, obtuse, and reflex angles. You will need a protractor to check the accuracy of the estimates.

 

Example 1

 

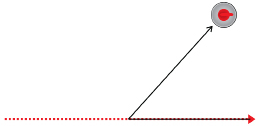
The illustration shows the path of a curling stone. Its original path is marked by red dots, and the angle of its deflection is marked as a black angle.

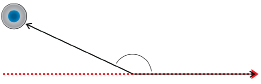
A curling stone strikes a rock in the house and is deflected from its original course.

  1. State whether the angle is acute, obtuse, or reflex.

  2. Estimate the angle at which the stone was deflected.

  3. Measure the angle to check your estimate.

Solution

  1. Because the angle is less than 90°, the angle is acute.

  2. The illustration shows the path of a curling stone. Its original path is marked by red dots, and the angle of its deflection is marked as a black angle. A blue square is placed with its lower right corner touching the vertex of the angle, and its base sits on the red dotted original path of the stone.

    If a square corner from a sheet of paper is placed on the figure as shown, the angle appears to be just a little larger than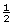 of a right angle. Since 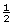× 90° = 45° (the referent), the angle may be 50° in measure.

  3. With a protractor, the angle measures 48°.

Example 2

 

The illustration shows a dotted path with an angle opening to the right.

A proton is fired from the left at the nucleus of a gold atom. The ray with the double arrow head shows the original course the electron would have taken in the absence of a collision. The electron is scattered from its original course as shown by the ray with the single arrow head.

  1. State whether the angle is acute, obtuse, or reflex.

  2. Estimate the scattering angle.

  3. Measure the angle to check your estimate.

Solution
  1. The angle is greater than 90° but less than 180°, so the angle is obtuse.

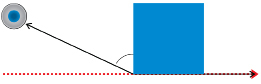
  2. The illustration shows a dotted path with an angle opening to the right. There is a blue square placed with its lower left corner on the vertex of the angle, and its base on the line that extends the dotted line.

    If the corner of a sheet of paper is placed on the angle, it looks as though the small angle between the dashed line and the arm of the angle is about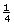 of a right angle (22.5° is the referent). So, the scattering angle is about 22.5° less than 180°. Since 180° – 22.5° = 157.5°, an estimate is 157°.

  3. Using a protractor, the angle measures 155°.
Example 3

 

A wrench is turned counterclockwise to loosen a bolt through an angle, as shown in the following graphic.

 

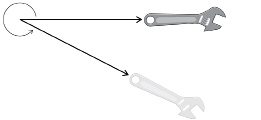
The illustration shows a wrench moved counterclockwise through an angle.

  1. State whether the angle is acute, obtuse, or reflex.

  2. Estimate the angle.

  3. Use a protractor to check your estimate.

Solution

  1. The angle is greater than 180° but less than 360°. The angle is a reflex angle.

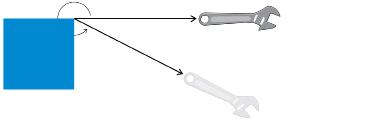
  2. The illustration shows an angle with a blue square placed with its top right corner on the vertex of the angle and its top sitting on the extension of the original arm of the angle.

    If the square corner of a sheet of paper is positioned at the vertex as shown, the small angle appears to be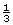 of a right angle (30° is the referent). So the reflex angle is about 30° less than one full rotation, 360° – 30° = 330°.

  3. Using a protractor, the small angle is 27°. So, the reflex angle is 333°.
Self-Check

 

Do these questions. When finished, check your answers.

 

Use these guidelines for each angle in the questions.

  1. Describe the angle as acute, right, obtuse, straight, reflex, or a full rotation.
  2. Use a referent to estimate the measure. State the referent you used: 22.5°, 30°, 45°, or 60°.
  3. Use a protractor to check your estimate.

SC 3. 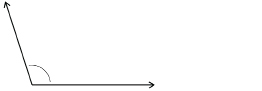The illustration shows an angle with one arm horizontal, and the other arm is rotated counterclockwise beyond the vertical.

 

SC 4. The illustration shows an angle with one arm horizontal, and the other arm is rotated clockwise beyond the vertical.

 

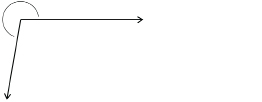
SC 5. The illustration shows an angle with one arm horizontal, and the other arm is rotated counterclockwise beyond the horizontal extension of the original arm.

 

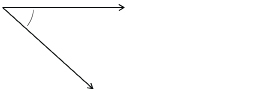
SC 6. The illustration shows an angle with one arm horizontal, and the other arm is rotated clockwise but not to a vertical position.

 

Compare your answers.

 

Mastering Concepts

 

You have seen that referents help in estimating the measure of an angle, but you can also estimate angles using a ruler.

 

Here is another method for estimating acute angles. You will need a ruler.

 

Step1: Draw any acute angle.

 

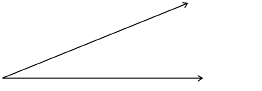
The illustration shows an acute angle.

 

Step 2: From the vertex, measure out 6 cm along each arm and mark these points A and B as shown.

 

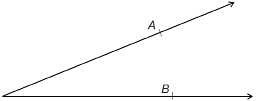
The illustration shows an acute angle with point A on one ray of the angle and point B on the other arm. Each marked point is 6 cm from the vertex.

 

Step 3: Measure the distance between A and B to the nearest tenth of a centimetre.

 

Step 4: Multiply the distance between A and B by 10. That is the measure of the angle within a degree or two. For example, if AB = 2.3 cm, then an estimate of the angle would be 2.3 × 10 = 23°.

 

Step 5: Check with a protractor to see how close the estimate is.

 

Use these steps with several acute angles. Then, answer the following questions to see why the steps work. When finished, check your answers.

 

MC 1. Points A and B are 6 cm from the vertex. If you drew a circle centred at the vertex and passing through A and B, what is the circle’s approximate circumference?

 

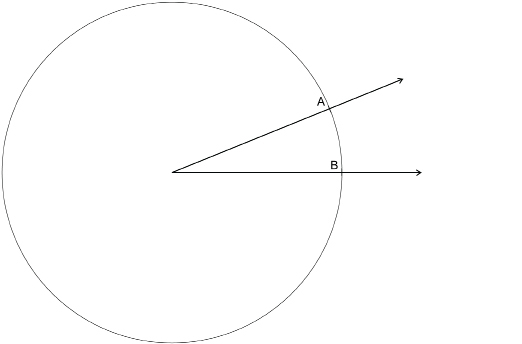
The illustration shows an acute angle with point A on one ray of the angle and point B on the other arm. Each marked point is 6 cm from the vertex. A circle is added with its centre at the vertex and passing through A and B.

 

MC 2. What is 10 times this circumference?

 

MC 3. How does the number of degrees in a circle compare to your answer in question MC 2?

 

Compare your answers.