1. Module 5

1.9. Page 4

Mathematics 10-3 Module 5 Lesson 2

 

 

Bringing Ideas Together

 

In Getting Started and Explore, you examined what it means to say that two or more angles are congruent. You saw that there are congruent angles all around you—in building design, in art, and in nature. Also, in Explore, you formed congruent angles through paper folding.

 

straightedge: a rigid strip of wood, metal, or plastic having a straight edge used for drawing lines

 

When a ruler is used without reference to its measuring scale, it is considered to be a straightedge.

In the next activity you will construct congruent angles using another approach—one that geometers have used for thousands of years. You will use your compass and a straightedge to draw congruent angles. Only after you are done will you use your protractor to measure the angles to check the accuracy of your construction.

 

But before you begin, review how to identify angles.

 

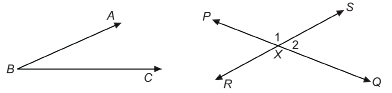
This is an illustration of an acute angle labelled ABC, which opens to the right, and an illustration of a pair of lines PQ and RS intersecting at point X.

 

If an angle stands alone as ∠ABC does, you may use a single letter to name it. ∠ABC and ∠B are the same angle. Notice that when a three-letter name is used, the middle letter is always the vertex. Likewise, the vertex is the only letter you can use for a single-letter name.

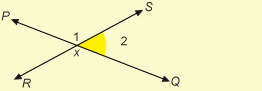
When there are two or more angles at a point, as when intersects at point X, confusion is possible. To distinguish among the angles, you must use a three-letter name or number the angles.

 

So at the intersection of the lines, ∠PXS is ∠1 and ∠QXS is ∠2.

 

Now use your compass and a straightedge to construct an angle congruent to ∠A.

 

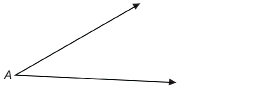
This illustration shows an acute angle labelled A that opens to the right.

 

Step 1: Draw a This will be the lower arm of the new angle. Notice that it does not have to point in the same direction as the lower arm of ∠A.

 

This illustration shows an acute angle labelled A that opens to the right, and a horizontal ray BC drawn to its right.

 

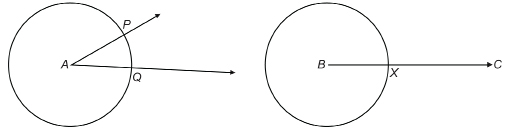
Step 2: Use your compass to draw circles with the same radius centred at A and at B.

 

The first circle cuts through the arms of ∠A at P and Q. The second circle cuts across at X.

 

This illustration shows an acute angle labelled A that opens to the right, and a horizontal ray BC drawn to its right. Added to the angle is a circle with centre A, which intersects the arms of the angle at P and Q. A circle with the same radius is shown drawn on ray BC with centre at B. It intersects the ray at X.

 

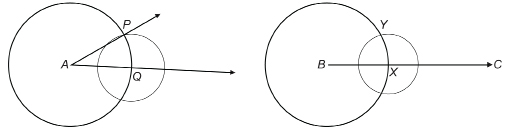
Step 3: With centre Q, draw a circle through P. With centre X and the same radius, draw a similar circle cutting the circle you drew in Step 2 at Y.

 

This illustration shows the same illustration as in Step 2 with a smaller circle drawn with its centre at Q and a radius of PQ. A circle with the same radius is drawn with its centre at X on ray BC. The intersection of the circles around ray BC is labelled Y.

 

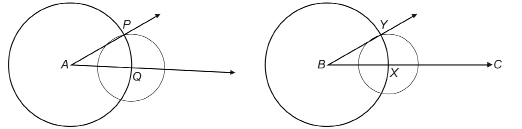
Step 4: Draw Use your protractor to check that

 

This illustration shows the same illustration as in Step 3 with ray BY drawn in.

 

Go to the applet “Constructing Congruent Angles” to view the construction of congruent angles demonstrating a compass and straightedge construction.

 

Self-Check

 

SC 1. Draw any obtuse angle. Then, with a compass and a straightedge, follow the steps you were just given to construct a second angle congruent to the obtuse angle. Then use a protractor to check whether your second angle is actually congruent to the first.

 

Compare your answers.

 

Stairs and Roofs

 

This is a photograph of a set of stairs.

© Mrfotos/shutterstock

 

In construction, carpenters use their carpenter squares to measure horizontally and vertically to obtain the angle required for projects such as stairs or roofs.

 

Think of a set of stairs.

 

The angle of the stairs does not change. Can you suggest a reason why?


 

 

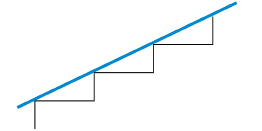
This illustration shows a set of uniform steps with a blue line drawn touching the top front edge of each step.

This uniformity guarantees that the angles are the same from step to step. You could lay a straight board on the steps to check. The board would rest on all the step edges.

 

The ratio of the riser height to the tread length affects the steepness or angle of the stairway. In other words, the vertical and horizontal measurements of a stairway affect its angle. Also for a roof, vertical and horizontal distances affect the angle of the roof.

 

The following is an example of how the slope of a roof can be determined from vertical and horizontal distances.

 

Example 1

 

This photo shows a house and attached garage under construction.© Jim Parkin/Fotolia.com

Akiko and her father are building a house and an attached garage. The slope of the garage roof is a 4-in rise for every 12 in measured horizontally.

  1. Draw a diagram of the roof using quarter-inch grid paper.

     

    You will need one sheet for the example and another sheet for the Self-Check.
  1. Measure the angle at which the roof rises.

Solution

 

Use one square to represent one inch.

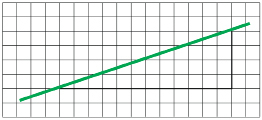
  1. This illustration shows a square grid with a horizontal line meeting a vertical line. A green line is added to obtain a right triangle with a length of 12 and a height of 4.

  2. Use your protractor to measure the angle.

    The angle of the roof is approximately 18.5°.

Self-Check

 

SC 2. For a roof that slopes at 45°, what is the rise (in inches) for a horizontal run of 12 in?

 

SC 3. Use grid paper to determine the angle at which a ladder rests against a vertical wall. The foot of the ladder is 3 ft from the wall, and the top of the ladder rests against the wall 8 ft above the ground.

 

Compare your answers.

 

Mastering Concepts

 

Try this question. To do this question you will need your protractor. When you are finished, check your answer.

 

Compare the following angles.

 

This illustration shows two angles labelled A and B. The drawn rays for angle B are longer than the rays for angle A.

 

Which of the following statements best describes the relationship between ∠A and ∠B?

  1. ∠A is smaller than ∠B.
  2. ∠A is congruent to ∠B.
  3. ∠A is larger than ∠B.

Justify your answer.

 

Compare your answers.

The steps are uniform. The treads, the part of the stairs you step on, are all the same size. The risers, the vertical portion of each step, are all the same size.