Module 5: Page 2 | MoodleHUB 🎓

1. Module 5

1.12. Page 2

Mathematics 10-3 Module 5 Lesson 1

Module 5: Angles

Get Started

bisect: to divide into two congruent (equal in measure) halves

bisector: a line or ray that divides a geometric shape into congruent halves

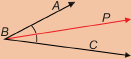
is a bisector of ∠ABC, since bisects ∠ABC into two congruent halves.

This is an illustration of an acute angle ABC bisected by ray BP, which is shown in red.

symmetry: the property of being the same size and shape on both sides of a central dividing line

Mike and Anna are discussing baseball. Anna plays baseball, and Mike has not really played, so Anna explains the game to Mike. She tells Mike that the lines running from home plate to the first and third bases form an angle. Anna explains to Mike that this angle is split into halves by the imaginary line running through second base, the pitcher’s mound, and home plate.

In the language of geometry, you could say that the ray from home base through the pitcher’s mound and second base bisects the larger angle. This ray is the bisector of the larger angle.

In their talk about baseball, Anna made Mike more aware of the bisector in a baseball diamond. Bisectors are a common feature not only in sports, but in design, nature, and art.

This is a picture of a model of the Avro Arrow with angles overlaid on the plane. The rays follow the forward edge of the wing and the fuselage.

National Film Board of Canada. Photothèque/Library and Archives Canada/
PA-111546

Look at the shape of the Avro Canada CF-105 Arrow. This fighter aircraft, designed in the 1950s, was considered the most advanced aircraft of its kind! Its delta-wing design illustrates a number of bisected shapes and angles. This is an example of symmetry.

This is a photo of a red maple leaf.

Nature provides examples of symmetry, too. For example, study the veins in a leaf. In a maple leaf, as in most other leaves, there is symmetry. One half of the leaf is the mirror image of the other half.

Can you sketch an angle and its bisector formed by the veins in the leaf?

Try This

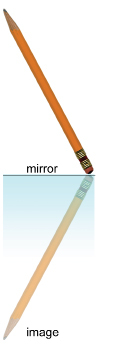
This illustration shows a pencil, a mirror, and the reflection of the pencil in the mirror from a viewpoint directly above the mirror.

In this activity you will bisect an angle using a mirror.

Step 1: Take a pencil and place one end against a mirror. Notice that the pencil and its image form an angle, with the vertex located at the point where the pencil touches the mirror.

Step 2: Change the size of the angle between the pencil and its image, all the while keeping the end of the pencil on the mirror. Then answer the following questions.

Save your answers to TT 1 and TT 2 in your course folder. You will be prompted to copy these answers to your Assignment Booklet later in this lesson.

TT 1. Where is the bisector of the angle formed by the pencil and its reflected image located?

TT 2. How is this demonstration with the pencil related to the concept described earlier with reference to the leaf and the design of the Avro Arrow?

The angles formed by the veins are bisected by the central vein running from the stem to the top of the leaf. An angle and its bisector are drawn on the leaf.

This is a photo of a red maple leaf with angle and bisector overlaid.