Module 5
1. Module 5
1.19. Page 4
Module 5: Angles
Bringing Ideas Together
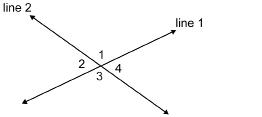
You worked with the angles in a triangle. You demonstrated that the sum of the angles is 180° by showing that these angles can be arranged to form a straight angle. You have also demonstrated that any pair of adjacent angles formed at the intersection of lines adds up to 180°. There is another angle relationship that is based on 180° and involves intersecting lines.
vertically opposite angles: angles lying across from each other at the point where two lines intersect
Vertically opposite angles are also referred to as opposite angles.
Line 1 and line 2 intersect to form two pairs of angles called vertically opposite angles or, simply, opposite angles. In the diagram, ∠1 and ∠3 are vertically opposite angles. Also, ∠2 and ∠4 are vertically opposite angles.
 Try This
Try This
In this activity you will explore how vertically opposite angles are related.
On the applet “Opposite Angles,” change the position of lines 1 and 2 to change the way the lines intersect.
Based on your investigation of vertically opposite angles in “Opposite Angles,” what conclusion could you make about the angles’ measures?
Answer the following questions to show, mathematically, how the sizes of the vertically opposite angles compare.
 Self-Check
Self-Check

First, you will show that ∠1 is congruent to ∠3.
SC 9. Complete the following statement. Then justify your answer.
∠1 + ∠2 = ____°.
SC 10. Complete the following statement. Then justify your answer.
∠3 + ∠2 = ____°.
SC 11. Using the results from SC 9 and SC 10, show (in a mathematical way) why ∠1 + ∠2 = ∠3 + ∠2.
SC 12. Use a similar approach to show that ∠2 is congruent to ∠4.
 Try This
Try This
TT 1. Next, you will demonstrate that opposite angles are congruent by folding paper.
Step 1: Draw a pair of intersecting lines on a blank sheet of paper. Label the opposite angles as shown.
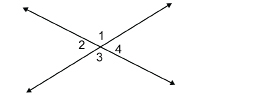
Step 2: Use your protractor to measure the opposite angles. What do you notice?
Step 3: Explain how to fold your sheet of paper to demonstrate that the opposite angles are congruent.
Using Angle Relationships
In the following examples and practice questions, you will apply the angle relationships you examined. These angle relationships will include the following angles in a triangle:
- vertically opposite
- adjacent
- complementary
- supplementary
Example 2
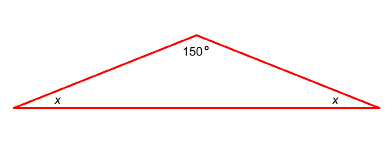
A student studying geometry in architecture used the following picture to illustrate the angles made by the roof of a structure.

© David Strand
The angle at the top of the roof was measured to be 150°. The two angles at the base are equal. What is the measure of each angle?
Solution
The sum of the measures of the three angles of the triangle is 180°. Therefore,
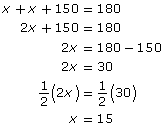
Check
![]()
Each angle at the base is 15°.
Sum of the Angles of a Triangle
Remember that when you rip off the corners of any triangle, you will see they form a line and add up to 180°.
Example 3
The W-type roof truss is the most common type of truss in simple wood-frame construction.
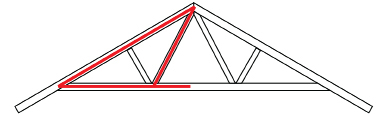
The angles will depend on the roof’s pitch. If the pitch of the roof is 32°, calculate the values of x and y.
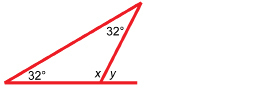
Solution
First, find the value of x.
The sum of the angles in the triangle is 180°.
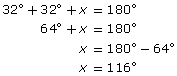
The angles with measures x and y are supplementary.
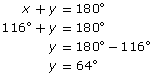
Example 4
Two straight paths cross at 30° as shown. Find the measures of the other three angles, which are represented by a, b, and c.
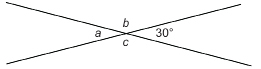
Solution
The angle with measure a is opposite the 30° angle. Therefore, a = 30°.
The angles with measures a and b are supplementary. So,
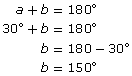
The angle with measure c is opposite b.
Therefore, c = b = 150°.
Example 5
Angles A and B are angles of a right triangle.
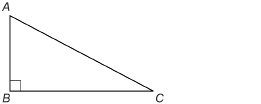
Show that ∠A and ∠C are complementary.
Solution
Watch “Lesson 4: Example 5 Solution.”
 Self-Check
Self-Check
Respond to the following questions.
SC 13.
- Name two pairs of complementary angles.
- Name one pair of supplementary angles.
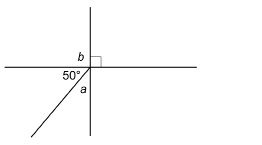
SC 14. Calculate the angle measures of a and b.
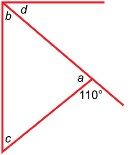
SC 15. Find the angle measures of a, b, c, and d for the rectangular envelope shown in the photograph. In the figure, ∠b = ∠c.

© mayamaya/shutterstock
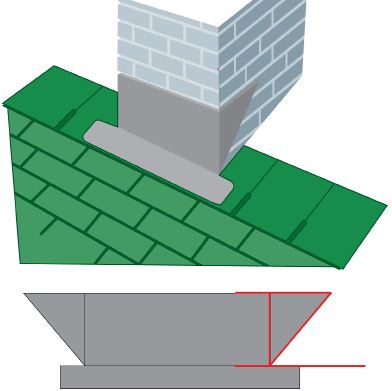
SC 16. The layout for a sheet-metal front-cap flashing to be positioned at the front of a chimney is shown. Find the missing measures a and b.
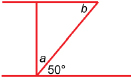
SC 17. Find the indicated measures.
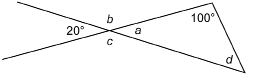
 Mastering Concepts
Mastering Concepts
Try this question. When you are finished, check your answer.
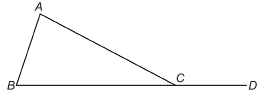
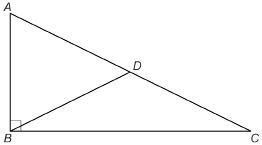
The angles within a triangle are called interior angles. If a side of a triangle is extended, an exterior angle is formed.
In ΔABC, ∠A, ∠B, and ∠ACB are interior angles. ∠ACD is an example of an exterior angle.
Show that the following is true: ∠A + ∠B = ∠ACD.