Lesson 2
1. Lesson 2
1.5. Explore
Module 3: Quadratics
Explore
You may have noticed when you were creating different graphs in the Discover section that the number of times the parabola touches or crosses the x-axis depends on whether the graph opens up or down and the location of the vertex (minimum or maximum value) of the graph.
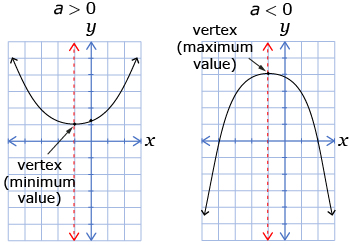
from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 323. Reproduced by permission.
If the value of a is positive, the graph will open upwards. If the value of a is negative, the graph will open downwards. In each case, the position of the vertex will determine whether there are two, one, or zero x-intercepts.
If a is positive, the graph opens upwards and the following statements are true:
- If the vertex is below the x-axis, there will be two x-intercepts because both arms of the parabola will cross the x-axis.
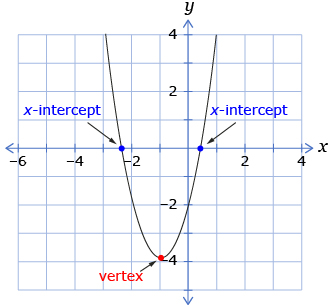
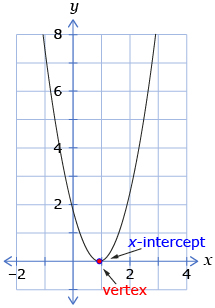
- If the vertex is on the x-axis, there will be one x-intercept because the parabola touches the x-axis at one point.
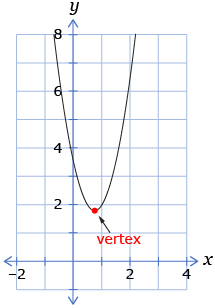
- If the vertex is above the x-axis, there will be zero x-intercepts because the parabola will never cross the x-axis.
If a is negative, the graph opens downwards and the following statements are true:
- If the vertex is below the x-axis, there will be zero x-intercepts because the parabola will never cross the x-axis.
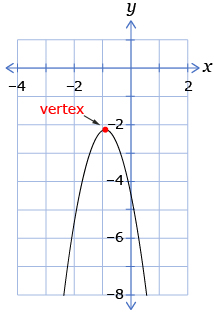
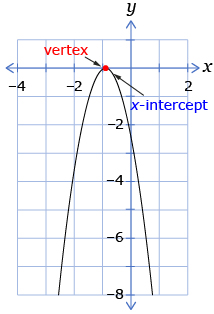
- If the vertex is on the x-axis, there will be one x-intercept because the parabola touches the x-axis at one point.
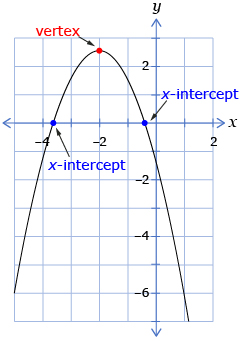
- If the vertex is above the x-axis, there will be two x-intercepts because both arms of the parabola will cross the x-axis.
If you are given the vertex and the direction of opening, can you decide how many x-intercepts the graph of the quadratic function will have?