Module 5
1. Module 5
1.24. Page 4
Module 5: Angles
Bringing Ideas Together
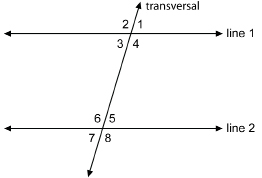
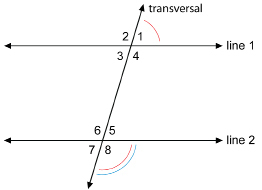
In the Explore section you compared the angles formed when two parallel lines are cut by a transversal. You should have discovered that vertically opposite angles are congruent.
In the diagram the vertically opposite angles are ∠1 and ∠3, ∠2 and ∠4, ∠5 and ∠7, and ∠6 and ∠8.
In TT 6 to TT 8 you compared the angles formed when two parallel lines are cut by a transversal. You discovered that angles in the same corresponding positions at the two points of intersection are congruent.
In the diagram, the corresponding angles are ∠1 and ∠5, ∠2 and ∠6, ∠3 and ∠7, and ∠4 and ∠8.
The applet “Corresponding Angles” highlights these angle relationships. Move the lines around by dragging the black dots on the line. Notice how the corresponding angles remain congruent.
Investigate the following questions as you explore “Corresponding Angles.”
-
How many different angle measures are there?
-
How does this number compare with the colouring diagram you did in the Share activity?
Now rotate the lines by dragging anywhere on the line except on the black dot. Watch for the answer to this question: Do the corresponding angles remain constant?
Example 1

© Lisa F. Young/shutterstock
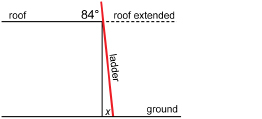
A ladder on level ground is propped against the side of a building with a flat roof (the roof is parallel to the ground). The angle between the ladder and the roof is 84°. What is the measure, x, of the angle between the foot of the ladder and the ground?
View the animated “Lesson 5: Example 1 Solution.”
Example 2

Jefferys, C. W. The Picture Gallery of Canadian History. Toronto: Ryerson Press, 1942. p 34. (left) Sparrow Illustration
Travois were used by people—like the Nehiyawak and the Siksika—on the plains and prairies to transport goods. Before the Spanish introduced the horse to North America, dogs were used to pull travois. A travois consisted of two poles lashed together and stabilized by one or more poles crossing the first two.
The following diagram matches the design of a travois.
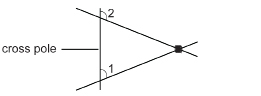
Classify ∠1 and ∠2. Are they congruent? Why or why not?
Solution
∠1 and ∠2 are corresponding angles because they lie in the same relative position at the cross pole.
They are not congruent because the other two poles (lines) are not parallel, as ∠1 is acute and ∠2 is obtuse.
Other Angles at the Transversal
In the Explore section you discovered that corresponding angles were not the only congruent pairs.
interior angles: angles lying between two lines cut by a transversal
exterior angles: angles outside two lines cut by a transversal
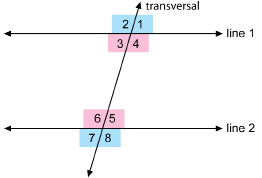
Look at the four angles between the parallel lines. ∠3, ∠4, ∠5, and ∠6 are interior angles.
The other four angles, ∠1, ∠2, ∠7 ,and ∠8, are exterior angles.
 Self-Check
Self-Check
SC 3. In the preceding diagram, which interior angles are congruent?
∠3 and ∠5 are alternate interior angles. ∠4 and ∠6 are also alternate interior angles, because they lie on alternate sides of the transversal.
Use the applet “Alternate Angles (of a Transversal)” to describe the relationship between alternate angles.
From the applet you can draw the following conclusions:
-
When two parallel lines are cut by a transversal, the alternate interior angles are congruent (equal in measure).
-
When two parallel lines are cut by a transversal, the alternate exterior angles are congruent (equal in measure).
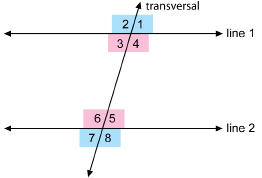
So, in the diagram, if the lines are parallel, the alternate exterior angles are congruent. The angles coloured pink are alternate exterior angles, so ![]() . Also, the angles coloured blue are alternate exterior angles, thus
. Also, the angles coloured blue are alternate exterior angles, thus ![]() .
.
Study these examples.
Example 3

© Paul.J.West/shutterstock
A wooden gate is crossbraced as shown. If the horizontal boards are parallel, determine the measure of the angle between one of the braces and the top horizontal board.
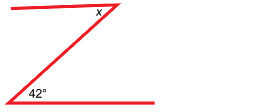
Solution
The two angles in the outline of the boards are alternate interior angles. The diagonal crossbrace is a transversal cutting across the parallel lines of the horizontal boards.
So, x = 42°.
Example 4

© Gulei Ivan/shutterstock
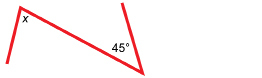
Classify the two angles in the diagram formed by the sides of the transmission tower and one of the diagonal braces. Do you have enough information to determine the value of x? Why or why not?
Solution
The angles in the outline are alternate interior angles. However, the sides of the tower are not parallel, so there is not enough information to find the value of x.
Another Angle Relationship
There is one more angle relationship that can be determined from the intersection of parallel lines by a transversal.
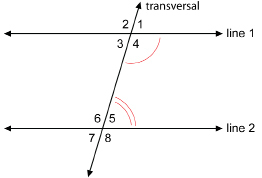
Consider the angle pair ∠4 and ∠5. What is the relationship between these two angles? The angles are not congruent, but a relationship does exist. Can you see it?
Use the applet “Transversal Angles” to help determine the relationship.
From the applet, you should have discovered that ∠4 and ∠5 are co-interior angles and are supplementary (add up to 180°). Consider this explanation as to why this is true.
The adjacent angles ∠1 and ∠4 form a straight angle—they are supplementary. So, ∠1 + ∠4 = 180°.
But ∠1 = ∠5, since they are corresponding angles. Therefore, you can substitute ∠5 for ∠1. So, ∠5 + ∠4 = 180°.
These two co-interior angles are supplementary. Similarly, the co-interior angles ∠3 and ∠6 are supplementary. So, ∠3 + ∠6 = 180°.
You may have noticed in the applet that co-exterior angles are supplementary if the lines are parallel.
![]()
Note: All of the angle relationships are reversible. If the corresponding angles are congruent, the lines are parallel. If the alternate interior or alternate exterior angles are equal, the lines are parallel. If the co-interior or co-exterior angles are supplementary, the lines are parallel.
Work through the following examples before you practise your skills.
Example 5
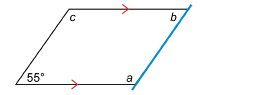
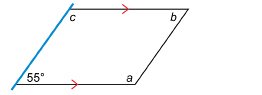
A cardboard box is partially flattened into a parallelogram, as shown in the diagram.
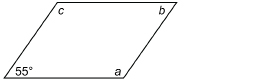
The angle at the lower left is 55°. Find the measures of the other three angles.
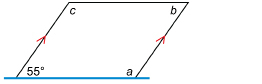
Solution
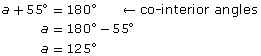
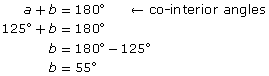
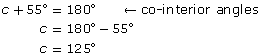
Example 6
Are line 1 and line 2 parallel? Why or why not?
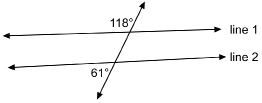
Solution
The given angles are co-exterior angles. If the lines were parallel, the co-exterior angles would be supplementary (add up to 180°).
Since 118° + 61° = 179°, line 1 and line 2 are not parallel.
Your turn!
 Self-Check
Self-Check
Complete the following questions.
SC 4. Play “Grocery Store Game (Exploring Parallel Lines).”
Try to collect at least 14 tokens. Select [Hints] if you need to review the meaning of vertically opposite, corresponding, and alternate angles. Consider a second game if you have trouble remembering the difference between vertically opposite, corresponding, and alternate angles.
SC 5. The following figure was found as a pattern in a painting.
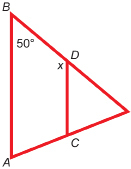
Based on the figure, answer the following questions:
-
Is
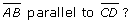 Justify your answer.
Justify your answer.
-
Calculate the value of x. State the angle property you used to justify your answer.
SC 6. This illustration shows a pair of vertical bridge supports and a crossbeam running from the top of one support to the base of the other. The angle between the second support and the beam is labelled x.

© basel101658/shutterstock
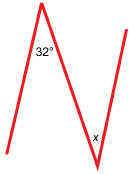
Calculate the value of x. Justify your answer. Assume the vertical bridge supports are parallel.
SC 7. Line 1 is parallel to Line 2.
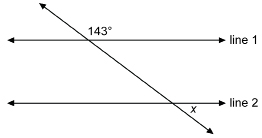
Find the value of x.
 Mastering Concepts
Mastering Concepts
Try this question. When you are finished, check your answer.
The angles within a triangle are called interior angles. If a side of a triangle is extended, an exterior angle is formed. In DABC, ∠A, ∠B, and ∠ACB are interior angles. ∠ACD is an example of an exterior angle.
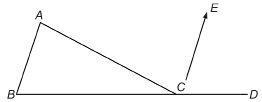
![]() Use parallel line relationships.
Use parallel line relationships.