Module 5
1. Module 5
1.29. Page 4
Module 5: Angles
Bringing Ideas Together
 Try This
Try This
In this multimedia piece you will explore the relationship between the sum of co-interior angles and the sum of co-exterior angles for parallel and non-parallel lines. As you explore this relationship between the sums, think about the following question.
Does the relationship between pairs of co-interior angles or pairs of co-exterior angles depend on the way the parallel lines are positioned on the plane?
TT 1. Go to “Exploring Parallel Lines—Explore It.” Click on “Explore It 2,” (in the middle of your screen), and follow the directions to complete the table that follows in this lesson.
Step 1: To begin, choose any transversal with parallel lines.
Step 2: Add the co-interior angles together, and record the sum in the table.
Step 3: Add the co-exterior angles together, and record the sum in the table.
Step 4: Repeat Steps 1 to 3 using parallel and non-parallel lines to fill in the table.
|
Sum of Co-Interior Angles |
Sum of Co-Exterior Angles |
|
|
Parallel Lines |
|
|
|
Example 1 |
|
|
|
Example 2 |
|
|
|
Non-Parallel Lines |
|
|
|
Example 1 |
|
|
|
Example 2 |
|
|
 Share
Share
You used “Exploring Parallel Lines—Explore It” to explore co-interior and co-exterior angles. You looked at both parallel and non-parallel lines. Share your results from TT 1 with a partner or a group, and then discuss the following question.
How does the way parallel or non-parallel lines are positioned on a plane affect the relationship between pairs of co-interior or co-exterior angles?
Write a one-sentence response to the discussion question. Save a copy of your response in your course folder.
In the Explore section of this lesson, you formed parallel lines by positioning supplementary angles along one side of a transversal. Then, in the Try This section, you saw that it does not matter which way the parallel lines are pointed on a plane. As long as the lines are parallel, the co-interior or co-exterior pairs add up to 180°.
These important relationships are summarized in the following information, and the relationships will be important as you solve problems later in this lesson.
|
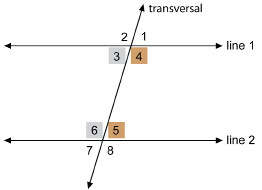
One of the co-interior pairs is ∠4 and ∠5. If those two angles add up to 180°, line 1 will be parallel to line 2.
Or, vice versa, if lines 1 and 2 are parallel, that makes ∠4 and ∠5 supplementary (the angles add up to 180°).
This is also true for the other pair of co-interior angles, ∠3 and ∠6. |
|
|
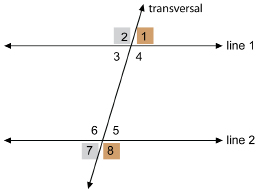
One of the co-exterior pairs is ∠1 and ∠8. If those two angles add up to 180°, line 1 will be parallel to line 2.
Or, vice versa, if lines 1 and 2 are parallel, then ∠1 and ∠8 will be supplementary (the angles add up to 180°).
This is also true for the other pair of co-exterior angles, ∠2 and ∠7. |
|
Two Lines and a Transversal
Examples 1 to 3 involve angle relationships for the following types of angles formed when two lines are cut by a transversal:
-
vertically opposite
-
supplementary
-
corresponding
-
alternate interior
-
alternate exterior
-
co-interior
-
co-exterior
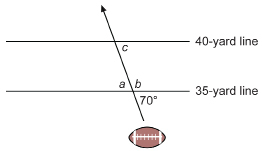
Example 1
A forward pass in football crosses the 35- and 40-yard lines as shown.
Determine the measure of angles a, b, and c. State the relationship you used to find each measure.
Solution
View the animated “Lesson 6: Example 1 Solution.”
Example 2
The outline of a kite is shown. Are the two edges drawn in red parallel? Justify your answer.
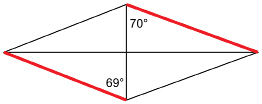
Solution
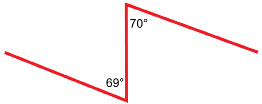
The 69° and 70° angles are alternate interior angles formed by the vertical transversal. As these angles are not congruent, the two red edges are not parallel.
Example 3
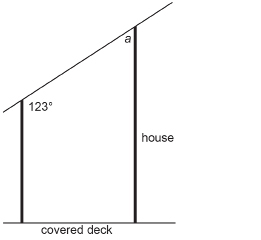

A covered deck is attached to the side of a house. Find the angle with measure a.
Solution
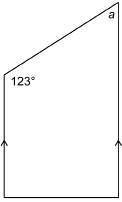

It is now your turn!
 Self-Check
Self-Check
Complete the following questions.
SC 7.

© Mark Stout Photography/shutterstock
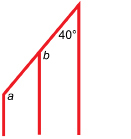
This illustration shows the measures of the angles in the overlay to the A-frame chalet’s windows. Find the missing measures for the windows of the chalet.
SC 8.
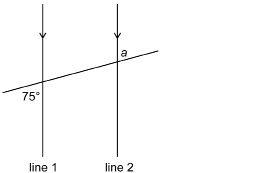
If line 1 is parallel to line 2, find a. What angle relationship did you use?
SC 9. Find the measure of ∠B.
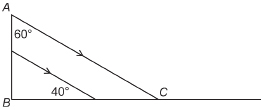
SC 10. ![]()
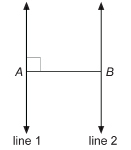
 Mastering Concepts
Mastering Concepts
Try this problem. When you are finished, check your answer.
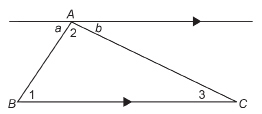
A line through point A is drawn parallel to the base of ![]() Without using a protractor, justify that the three angles of
Without using a protractor, justify that the three angles of ![]() add up to 180°.
add up to 180°.