Module 6
1. Module 6
1.13. Page 3
Module 6: Triangles and Other Polygons
Explore
In the previous lessons you explored a variety of methods for drawing similar polygons. Now you will explore three additional methods for drawing similar triangles.
 Try This
Try This
Work with a partner, if possible.
Method 1: Constructing Congruent Angles
Step 1: Draw any ![]()
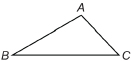
Step 2: Use your ruler to draw the base ![]() of
of ![]() This base can be any length. If you want the sides of
This base can be any length. If you want the sides of ![]() to be twice as long as those of
to be twice as long as those of ![]() you would make
you would make ![]() But any length will do.
But any length will do.
Note: Using the names ![]() (instead of completely different letters) to label the new triangle makes it easy to see the pairs of corresponding angles that are the same size. In addition, this way of labelling makes it clear which sides correspond to one another.
(instead of completely different letters) to label the new triangle makes it easy to see the pairs of corresponding angles that are the same size. In addition, this way of labelling makes it clear which sides correspond to one another.
Step 3: Use your protractor to draw angles at ![]() congruent to
congruent to ![]() Call the point where these angles’ arms cross point
Call the point where these angles’ arms cross point ![]() Join
Join ![]()
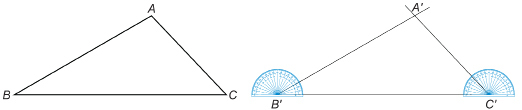
Now you will check whether the two triangles are similar.
TT 4. You used your protractor to make the corresponding angles congruent. That is, you made ![]() Now listen to “How to Read a Symbolic Geometric Statement.”
Now listen to “How to Read a Symbolic Geometric Statement.”
Why must ![]() Check
Check ![]() with your protractor to see if
with your protractor to see if ![]() Record those measures on your diagram.
Record those measures on your diagram.
TT 5. Now you will check to see if the ratios of the corresponding sides are equal. Measure, and then record on your diagram, the lengths, to the nearest millimetre, of the sides of both triangles.
Calculate and compare ![]() Are the triangles similar?
Are the triangles similar?
Method 2: Constructing Proportional Sides
Step 1: Draw any ![]()

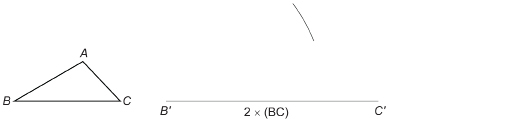
Step 2: Decide what ratio you wish to use. If you want a similar triangle with sides twice as long, begin by measuring the base BC. Then draw base ![]() twice as long as BC.
twice as long as BC.

Step 3: Measure AB. Then set your compass to a radius twice as large. With ![]() as centre, draw an arc where
as centre, draw an arc where ![]() is likely to be.
is likely to be.
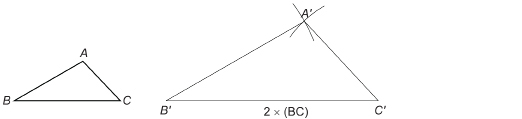
Step 4: Measure AC. Then set your compass to a radius twice as large. With ![]() as centre, draw an arc intersecting the first arc. Call this point
as centre, draw an arc intersecting the first arc. Call this point ![]() Join
Join ![]()
TT 6. You decided to make the sides twice as long, but you could have used any ratio—three times, one-half, or any value of your choosing. You know the sides are proportional, but are the corresponding angles congruent? Measure the angle pairs. Record their measures on your diagram. Are the triangles similar? Explain your answer.
Method 3: Constructing One Pair of Congruent Angles and Two Pairs of Proportional Sides Forming That Angle
This method is often used if the two triangles share an angle.
Step 1: Draw any triangle ABC.
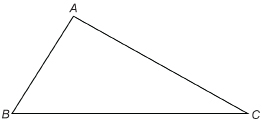
Suppose you want the second triangle to share ![]() Also suppose that you want the sides of the second triangle to be one-third as long as the sides of
Also suppose that you want the sides of the second triangle to be one-third as long as the sides of ![]()
Step 2: Measure AB. Divide that length by 3. Measure out that distance from point A along AB. Call that point ![]() So,
So, ![]()
Step 3: Measure AC. Divide that length by 3. Measure out that distance from point A along AC. Call that point ![]() So,
So, ![]()
Step 4: Join ![]()
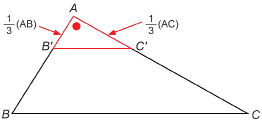
![]()
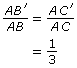
But are ![]() similar? To find out, answer these questions.
similar? To find out, answer these questions.
TT 7. ![]()
TT 8. ![]()
TT 9. ![]()
TT 10. Are ![]() and BC parallel? Justify your answer.
and BC parallel? Justify your answer.
TT 11. Which method of drawing similar triangles makes the most sense to you? Why?
 Share
Share
It is time to share your answers to TT 4 to TT 11. Remember that sharing work is an important part of learning. To make the most of your sharing opportunity, be sure that you do the following:
-
Check that you have completed TT 4 to TT 11 to the best of your ability and have the answers in a form that you can easily share with another student, or with your teacher, if so directed.
-
Use the discussion area for your class, or another method indicated by your teacher, to post your answers to TT 4 to TT 11 and to view the work of the people with whom you are sharing.
-
Compare answers for TT 4 to TT 11. Identify where you have similar answers and where your answers are different. Discuss all differences between your answers until you have an agreement. If necessary, you may wish to involve your teacher in your discussion.
-
Revise your answers to TT 4 to TT 11 where necessary.
Save the revised copy of your work, including your diagrams, in your course folder. Ask your teacher whether you are to save a transcript of your discussion in your course folder as well.