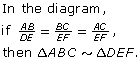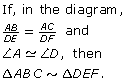Module 6
1. Module 6
1.14. Page 4
Module 6: Triangles and Other Polygons
Bringing Ideas Together
In the Explore section, you investigated three methods for drawing similar triangles. These methods are based on the three conditions listed in the following table.
TRIANGLE CONDITIONS FOR SIMILARITY
|
Graphic Representation |
Description in Words |
Symbolic Description |
Nickname |
|
Condition 1
|
If the corresponding angles of two triangles are equal in measure, then the triangles are similar. |
|
e.g., AAA Similarity |
Condition 2
|
If the corresponding sides of two triangles are proportional, the triangles are similar. |
|
|
Condition 3
|
If two pairs of sides of two triangles are proportional, and the angles between those pairs of sides are congruent, the triangles are similar. |
|
|
Nicknames for the conditions may help you keep the three conditions straight. A possible nickname is provided in the table for Condition 1.
On a copy of “Triangle Conditions for Similarity,” fill in your own nicknames for the conditions.
Place your completed table in your course folder.
Note: When two figures are similar, you can use the symbol ~ to replace the words “is similar to.”
The following examples show how these conditions can be used to solve problems involving similar triangles.
Example 2: Using Condition 1
A 3-m pole and a 4-m pole are leaning against a vertical wall. Each pole makes an angle of 80° with the ground.
- Are the triangles formed by the poles similar? Why?
- If the 4-m pole reaches 3.94 m up the wall, how far up the wall does the 3-m pole reach?
Solution
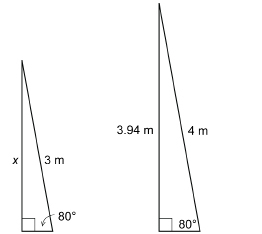
Assume the vertical wall is perpendicular to the ground. All of the corresponding angles are equal.
The two 80° angles are equal in measure. The two right angles are equal in measure. So, the third angle in each triangle must be 10°, since 10° + 80° + 90° = 180°.
Note: This example confirms the fact that if two pairs of angles are equal in measure (congruent), so too is the third pair.
As the three pairs of corresponding angles are congruent, these triangles are similar.
- As the triangles are similar, the sides are proportional.
Let x be the height up the wall the 3-m pole reaches.
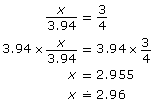
The 3-m pole reaches approximately 2.96 m up the wall.
Example 3: Using Condition 2
Two triangular sails from a model ship have the following dimensions.
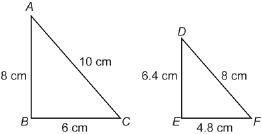
Are the corresponding angles congruent?
Solution
Use the indicated lengths of the sides to see if corresponding sides are proportional.
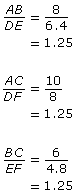
Because the ratios are equal, the triangles are similar.
Since ![]() the corresponding angles are congruent.
the corresponding angles are congruent.
Example 4: Using Condition 3
In the following figure there are two triangles—one triangle is inside the other.
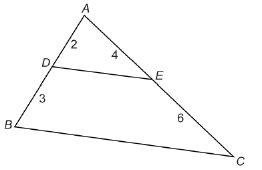
Is ![]()
View the animated “Example 4 Solution: Finding Lengths in Similar Triangles.”
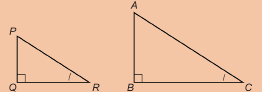
Similar Right Triangles
From a couple of the examples involving right angles, you may have noticed this condition—if just one pair of corresponding acute angles are equal in measure, the triangles are similar.
More generally, for any two triangles, if two pairs of corresponding angles are equal in measure, the triangles are similar.
This general statement can be represented this way.
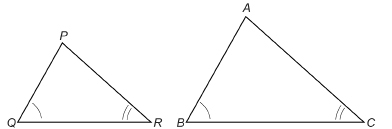
The general statement follows from Condition 1. Why?
![]()
The reasoning is this: If triangles PQR and ABC have two pairs of angles that are equal, the other pair of angles must also be equal because the angles in each triangle must add up to 180°.
 Self-Check
Self-Check
SC 4. Jill said to her partner, “For any two triangles, if two pairs of corresponding angles are equal in measure, the triangles are similar.”
Harlon said that, from Jill’s statement, he could then conclude the following about right triangles:
For right triangles, if just one pair of corresponding acute angles are equal in measure, the right triangles are similar.
How could Harlon make this conclusion about right triangles?
SC 5. Look at ![]() in the following diagram.
in the following diagram.
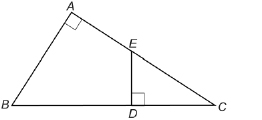
Are ![]() similar? Why or why not?
similar? Why or why not?
SC 6. Name the equal ratios in SC 5. If there are none, explain why there are none.
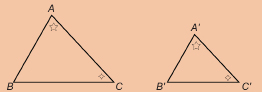
SC 7. In the following diagram, ![]()
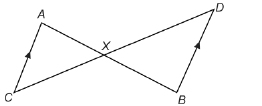
Are ![]() similar? Why or why not?
similar? Why or why not?
SC 8. Look at the following triangles.
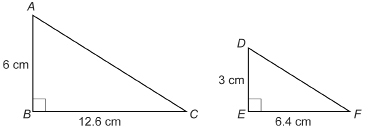
Are ![]() similar? If they are, explain why they are. If they are not, what change could you make in one or more of the measures given so that the triangles would be similar?
similar? If they are, explain why they are. If they are not, what change could you make in one or more of the measures given so that the triangles would be similar?
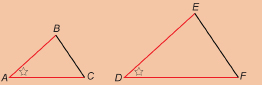
SC 9. Identify ![]() in the diagram.
in the diagram.
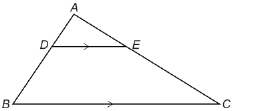
Suppose ![]() Are
Are ![]() similar triangles? Why or why not?
similar triangles? Why or why not?
SC 10. Expand your copy of the table “Triangle Conditions for Similarity,” presented near the beginning of this lesson, to include the two new conditions explored in this Self-Check activity. You should have a copy of this table in your course folder; if not, go to “Triangle Conditions for Similarity” for another copy.
|
Graphic Representation |
Description in Words |
Symbolic Description |
Nickname |
|
Condition 4
|
|
|
|
|
Condition 5
|
|
|
|
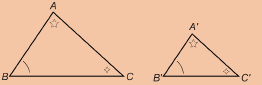
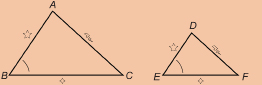
SC 11. Which diagram makes it easier to see the corresponding parts of the two triangles? Explain your answer.
 Mastering Concepts
Mastering Concepts
Try this question. When you are finished, check your answer.
The diagram shows ![]() .
. ![]() joins point D on side AB with point E on side AC.
joins point D on side AB with point E on side AC.
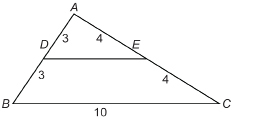
- In the diagram, is
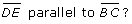 Why or why not?
Why or why not? - What is the length of