Module 6
1. Module 6
1.17. Page 2
Module 6: Triangles and Other Polygons
Get Started
In this activity you will review how to handle proportions involving more than one measurement unit.
 Self-Check
Self-Check
Work with a partner, if possible.

© Walter Quirtmair/21324926/Fotolia
Consider the following two similar triangles. A shed of unknown height, x, casts a shadow measuring 12 ft 6 in. At the same time, a 2-ft vertical post casts a shadow measuring 3 ft 3 in.
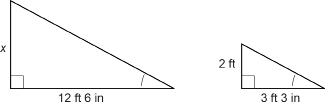
How would you set up and solve a proportion to determine the height of the shed?
Method 1
First convert all measures to feet. Recall that 1 ft = 12 in.
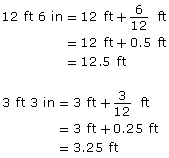
Set up the proportion.
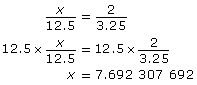
The height is approximately 7.7 ft.
Method 2
First convert all measures to inches. Then solve for x by answering SC 1 through SC 3.
SC 1. What are the measures in inches?
SC 2. Set up a proportion and solve for x in inches.
SC 3. Convert your SC 2 answer from inches to feet. Round to one decimal place.