Module 6
1. Module 6
1.22. Page 2
Module 6: Triangles and Other Polygons
Get Started

Courtesy of Ken Allred
In the next part of the lesson you will examine a method for determining a right angle. Also, you will review solving simple equations involving squares and square roots.
Five thousand years ago or more, the annual flooding of the Nile made it necessary to resurvey property lines and replace boundary markers. Early Egyptian surveyors were called rope stretchers because of their use of knotted ropes to measure distance and determine angles.
One method these surveyors used was to stretch a looped rope with 12 equally spaced knots. You will be an Egyptian rope stretcher after you complete the following Try This activity.
 Try This
Try This
Work with a partner, if possible.
Instead of using a rope, it will be easier to use paper strips. Print a copy of “Half-Inch Grid Paper.”
Step 1: Cut 12 strips from the grid paper. The strips should be cut lengthwise from the page and measure one square in width. Each strip will be 11 in long and ![]() in wide. Glue the strips end-to-end, overlapping each strip approximately
in wide. Glue the strips end-to-end, overlapping each strip approximately ![]() in. Continue taping the strips until you have formed a loop. Be careful not to have any twists in the loop.
in. Continue taping the strips until you have formed a loop. Be careful not to have any twists in the loop.
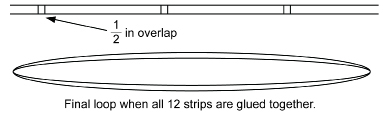
Step 2: With your marker, carefully mark a vertical line down the middle of each overlap.
![]()
When finished, you will have created a loop with 12 equally spaced vertical lines—similar to the Egyptian looped rope with 12 equally spaced knots. Think of your loop as 12 units in circumference with the distance between two consecutive marks being 1 unit.
Step 3: With your partner, stretch the loop on the floor to form a triangle measuring 3 units on one side, 4 units on a second side, and 5 units on the third side. You will be able to do this, because 3 units + 4 units + 5 units = 12 units.
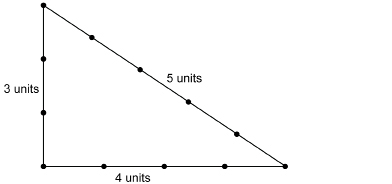
If you have a carpenter’s square, check to see how close the angle formed by the 3-unit and 4-unit sides is to a right angle.
Pythagorean triple: three whole numbers that represent the lengths of the sides of a right triangle
There are an infinite number of such triples.
The ancient Egyptians, as well as the Babylonians and Chinese, among others, knew that a 3-4-5 triangle formed a right angle. Today, such a triple is called a Pythagorean triple.
Another fact the Egyptians and others knew was that if squares were constructed on the sides of a right triangle, the area of the largest square would be exactly equal to the areas of the two smaller squares added together.
Look at the following squares constructed on the sides of a 3-4-5 right triangle.
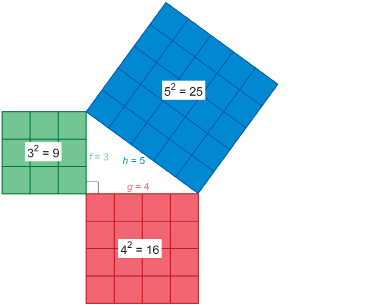
As you can see,
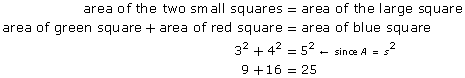
Pythagorean Theorem: For any right triangle, the square on the hypotenuse is equal to the sum of the squares on the two legs.
hypotenuse: in a right triangle, the side opposite the right angle; the longest side in a right triangle
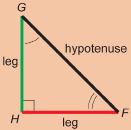
leg: one of the two sides of a right triangle that forms the right angle
As you saw above, the 3-4-5 right triangle side relationship can be represented by 32 + 42 = 52. That is just one instance of the Pythagorean Theorem.
 Try This
Try This
In the “Pythagorean Theorem Demonstration Applet,” change the leg lengths by pulling the corners of the triangle. Use the “hide areas” and “show areas” buttons to help fill in the following table for any three different triangles you make.
INVESTIGATING RIGHT TRIANGLES
|
Lengths |
Area of Squares |
Sum of Squares of Legs |
||||
|
Leg (f) |
Leg (g) |
Hypotenuse (longest side) (h) |
Leg (f 2) |
Leg (g2) |
Hypotenuse (h2) |
f 2 + g2 |
TT 1. Do the squares of the leg sides always add up to equal the square of the hypotenuse side—is f 2 + g2 = h2 true in each case?
TT 2. Hand draw a triangle where the Pythagorean Theorem would NOT apply. Add the measurements of this triangle and the calculations to the chart too. Is this a right triangle? Is f 2 + g2 = h2 true for this triangle?
 Share
Share
It’s time to share your data from the “Investigating Right Triangles” table and your answers to TT 1 and TT 2 with others. Compare your answers and revise them if necessary. If you still need help, ask your teacher. Save the revised copy of your work in your course folder.
You may have noticed that the applet only let you make right triangles. This is because the Pythagorean Theorem only applies to right triangles, making it a great technique for checking to see if you have a right triangle!
In the applet “Pythagorean Theorem,” you examined many possibilities for the right triangle. For some, the sides were whole numbers, as in the 3-4-5 right triangle. In others, the sides were decimal approximations. In all cases, the calculations were done automatically for you. However, you will be required to perform the calculations yourself. The following example will help you remember a few basics about equations and using your calculator.
Example 1
If the legs of a right triangle are 6 cm and 8 cm, what is the length of the hypotenuse?
Solution
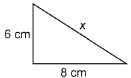
![]()
To evaluate ![]() on your calculator, strike these keys.
on your calculator, strike these keys.
![]()
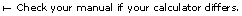
![]()
To evaluate ![]() on your calculator, strike these keys.
on your calculator, strike these keys.
![]()
![]()
Your calculator will tell you that ![]() .
.
If you had difficulties following the solution on your calculator, ask your teacher for help.
 Self-Check
Self-Check
Try these questions.
SC 1.
Solve ![]()
SC 2.
Solve ![]()