Module 6
1. Module 6
1.23. Page 3
Module 6: Triangles and Other Polygons
Explore

Photos.com/Thinkstock
In the Get Started section, you reviewed the essentials of the Pythagorean Theorem. This theorem is named after Pythagoras of Samos, a Greek philosopher and mathematician who lived from about 570 BCE to 490 BCE.
Even though Pythagoras spent a great deal of his life on the Greek island of Samos, he did study in Egypt and would have been familiar with the work of the rope stretchers. Pythagoras is credited with deriving formal proof for the relationship among the sides of the right triangle.
In spite of the fact that this theorem bears his name, you should remember that mathematicians in China, India, and Babylon applied this relationship almost two thousand years earlier. Ideas flowed from culture to culture. Mathematics is not unique to a specific people or time; rather, mathematics is a human endeavour.
In this activity you will explore a proof from China that was known at least 500 years before Pythagoras.
 Try This
Try This
Work with a partner, if possible.
Print a copy of “Pythagorean Theorem Master.”
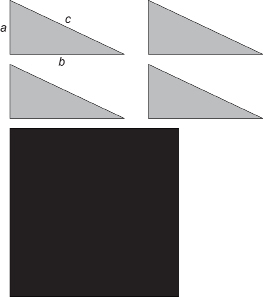

Step 1: Cut out the four identical, grey right triangles and the black square. Place the four triangles on top of the black square as shown below.
Step 2: Pencil a, b, and c along the sides of each triangle to help answer the following questions. Notice that the lengths of the sides of the original big black square equals a + b, the sum of the legs of each triangle.

TT 3. The black figure in the middle of the triangle arrangement appears to be a square. Without measuring, explain how you know that each of the four angles of the black figure is a right angle and how you know the sides are all equal.
TT 4. What is the area of the black square showing in the middle of the arrangement? Is it a2, b2, or c2? Why?
After recording your responses, continue to Step 3.
Step 3: Rearrange the four grey right triangles on the original, larger black square as shown.
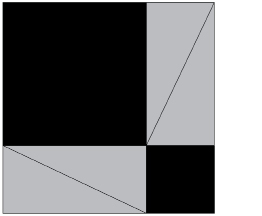
TT 5. Why must the total area of the black areas showing in this arrangement be the same as the black area showing in the first arrangement?
TT 6. The two black figures shown in this arrangement look like squares. However, how do you know that the two black figures are actually squares?
TT 7. What is the area of the larger black square? Is it a2, b2, or c2? Why?
TT 8. What is the area of the smaller black square? Is it a2, b2, or c2? Why?
TT 9. What is the total of the areas of the two black squares?
TT 10. How is your answer to TT 9 related to your answer to TT 4? Write out the relationship. Where have you seen this relationship before?
You have just proven the Pythagorean Theorem.
 Share
Share
In Explore you investigated an ancient proof of the Pythagorean Theorem. There are many proofs of the Pythagorean Theorem that involve cutting out pieces and rearranging them as you did in Explore.
Find another such physical proof by doing an Internet search. Share the link to the proof and a quick summary with other students in your class. Read through the proofs found by other students, and choose a proof to try.
Save your work in your course folder. You will be asked to include an outline of the physical proof and a description of any pieces you cut out and rearranged in the Lesson Assignment. Include diagrams or photos to show your proof.