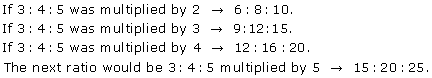Module 6
1. Module 6
1.24. Page 4
Module 6: Triangles and Other Polygons
Bringing Ideas Together
In the Explore section you proved the Pythagorean Theorem. The statement of the theorem applied to a right triangle is labelled below. The length of the hypotenuse is c. The lengths of the legs are a and b.
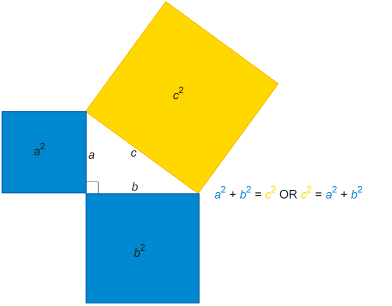
Remember, the Pythagorean Theorem only applies to right triangles, as you discovered in the Get Started section. It states that for any right triangle, the square on the hypotenuse equals the sum of the squares on the two legs.
The letters used in the statement depend on the labels on the sides of the triangle.
Example 2
Write the statement of the Pythagorean Theorem for each right triangle.
Solution
- Notice that, here, the lengths of the sides of the triangle are named using lowercase (small) letters. The letter used depends on the opposite angle.
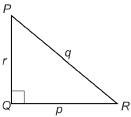
The length of side QR is p, because this side lies opposite ∠P.
The length of side PR is q, because this side lies opposite ∠Q.
The length of side PQ is r, because this side lies opposite ∠R.
Because q is the length of the hypotenuse, q2 = p2 + r2, or p2 + r2 = q2.
- Once again, the lengths of the sides of the triangle are named using lowercase (small) letters. Again, the letter used depends on the opposite angle.
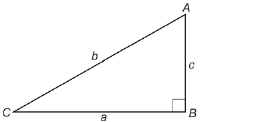
The length of side BC is a, because this side lies opposite ∠A.
The length of side AC is b, because this side lies opposite ∠B.
The length of side AB is c, because this side lies opposite ∠C.
Because b is the length of the hypotenuse, b2 = a2 + c2, or a2 + c2 = b2.
The Carpenters’ Corner
In Get Started, you stretched a paper loop to form a 3-4-5 right triangle. This Pythagorean triple is used by carpenters to check that corners are square. Carpenters will mark points 3 ft and 4 ft from the corner.
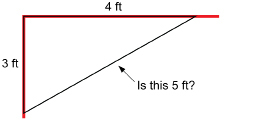
If the distance between the marks is 5 ft, the corner is square.
Because triangles with proportional sides are similar, the following side-length ratios will all be Pythagorean triples!
3:4:5
6:8:10
9:12:15
12:16:20
Do you see the pattern here? How would you find another Pythagorean triple with this same ratio?
 Self-Check
Self-Check
SC 3.
- Show that 5, 12, 13 is a Pythagorean triple.
- Sketch a triangle with these sides.
- From 5, 12, 13, write three more Pythagorean triples.
SC 4.
- Is 4, 7, 9 a Pythagorean triple?
- Sketch a triangle with these sides.
- Is the triangle a right triangle? Why or why not?
Example 3
A ladder is leaning against a vertical wall. The foot of the ladder is 1 m from the wall, and the ladder reaches 3 m up the wall. How long is the ladder? Round to 1 decimal place.
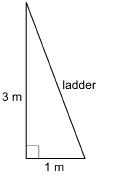
Solution
Let the length of the ladder be x.
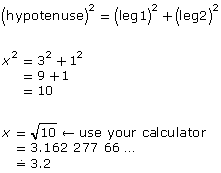
The ladder is about 3.2 m in length.
 Self-Check
Self-Check
SC 5. Kale walked 300 m north, turned, and then walked 200 m east. How far is Kale from his starting point? Round your answer to the nearest metre.
 Mastering Concepts
Mastering Concepts
Try this question. When you are finished, check your answer.
The numbers 3, 4, and 5 form a Pythagorean triple. Prove that the triplet 3n, 4n, 5n, where n is any positive whole number (n = 1, 2, 3, or 4, and so on), is also a Pythagorean triple.