Module 6
1. Module 6
1.29. Page 4
Module 6: Triangles and Other Polygons
Bringing Ideas Together
In the Explore section you investigated how the Pythagorean Theorem may be used to verify whether a given triangle is a right triangle.
The Pythagorean Theorem states that, for any right triangle, the square on the hypotenuse is equal to the sum of the squares on the two legs.
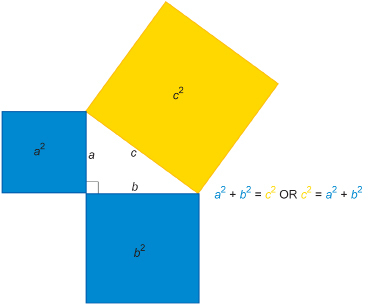
The Pythagorean Theorem also states that if the square on the longest side of a triangle is equal to the sum of the squares on the other two sides, then the triangle is a right triangle. The longest side will be the hypotenuse. The angle opposite the longest side will be a right angle. So, the following are both true and useful when problem solving.
![]()
![]()
You are now ready to apply the Pythagorean Theorem to problem situations.
Example 1
The sides of ![]() are a = 5 cm, b = 8 cm, and c = 7 cm.
are a = 5 cm, b = 8 cm, and c = 7 cm.
- If
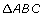 were a right triangle, which side would be the hypotenuse? Why?
were a right triangle, which side would be the hypotenuse? Why? - Is
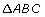 a right triangle? Why or why not?
a right triangle? Why or why not?
Solution
- The hypotenuse would be the longest side, b.
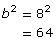
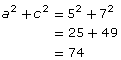
Since the square on the longest side is not equal to the sum of the squares on the two other sides, is not a right triangle.
is not a right triangle.
Example 2

© Westfield. Reproduced with permission.
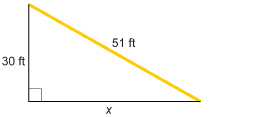
A 51-ft grain auger is backed up to a 30-ft-tall grain bin as shown in the illustration.
How far from the bin is the foot of the auger? Round your answer to the nearest foot.
Solution
Let the distance to the bin be x.
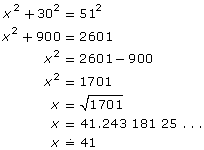
The foot of the auger is approximately 41 ft from the bin.
Example 3
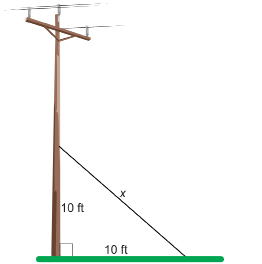
A guy wire supporting a power pole is anchored 10 ft up the pole and, at the ground, 10 ft from the pole.
Correct to one decimal point, what is the length of the guy wire?
Solution
Let x be the length of the guy wire.
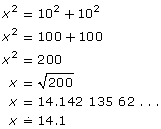
The guy wire is approximately 14.1 ft in length.
 Self-Check
Self-Check
Try these questions.
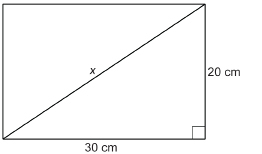
SC 4. What is the longest metal rod that will lie flat on the bottom of a rectangular box 20 cm wide and 30 cm long? Express your answer to the nearest centimetre.
SC 5. Maxim is cycling in the country. He travels 2 mi north along a range road and then 1 mi west along a township road.
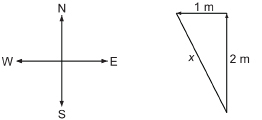
To the nearest tenth of a mile, how far is Maxim from his starting point?
SC 6. A kite is being flown over a school 100 m away.
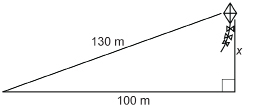
In reaching this position, 130 m of string has been let out. How high above the ground is the kite? Round to the nearest metre.
SC 7. The interior of a rectangular sewing box is 15 cm wide, 20 cm long, and 16 cm high. Can a knitting needle
28 cm long be placed in the box without sticking out of the top?
Mastering Concepts

iStockphoto/Thinkstock
Try this question. When you are finished, check your answer.
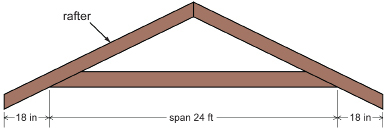
Anya is helping her father build a garage. They have seen W-trusses used in the construction of several garages in the neighbourhood. They also plan to use W-trusses to support the roof. Such trusses are shown here against the open sky before the roof is attached.
Anya wants to calculate the length the rafters (the sloping beams of the trusses) will have to be. Each truss must span 24 ft—the width of the garage—and have an 18-in overhang beyond each wall, as shown in the diagram.
The roof has a slope of 4 in for a horizontal run of 12 in. This slope is represented by the triangle in the following diagram.
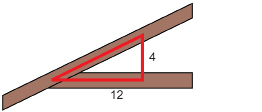
Help Anya find the length of each truss to the nearest sixteenth of an inch.