1. Module 7

1.2. Page 2

Mathematics 10-3 Module 7 Lesson 1

Module 7: Trigonometry

 

Get Started

 

clinometer: a device for measuring angles to distant objects that are higher or lower than your position

In the following Try This Activity you will make a “Clinometer.”

 

Try This

 

Work with a partner, if possible.

 

Step 1: Print a copy of Clinometer Template.

 

This is a graphic of a clinometer template.

 

Step 2: Glue the template to a sheet of cardboard. Then cut out the semicircular protractor.

 

Step 3: Tape a drinking straw to the base of the protractor as shown.

 

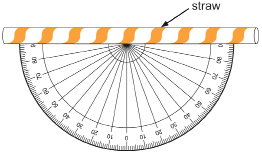
This illustration shows a straw mounted to the base of a protractor.

 

Step 4: Poke a small hole through the crosshairs at the centre of the protractor’s base. Pass one end of your thread through the hole. Knot and tape that end of the thread so it will not slip back through. Tie a weight (like a penny) to the free end of the thread.

 

This illustration shows a straw mounted to the base of a protractor and a string tied to the crosshair point of the protractor. A weight is attached to the end of the string.

 

Step 5: Let the weight swing free. When the straw is horizontal, the thread should lie along the 0° line, as shown in the diagram.

 

angle of elevation: an angle through which you must rotate the clinometer from the horizontal to see a higher object

When you look through the straw at an object higher than you are, your partner should be able to read the angle of elevation from the scale when the weight hangs down and is motionless.

 

 

This illustration shows the clinometer pointing slightly upward to a distant object. The string is hanging straight down, and an arrow points to the point where the string crosses the protractor. The arrow is labelled “Read angle here.”

 

angle of depression: an angle through which you must rotate the clinometer from the horizontal to see a lower object

When you look through the straw at an object lower than you are, your partner should be able to read the angle of depression from the scale when the weight hangs down motionless.

 

 

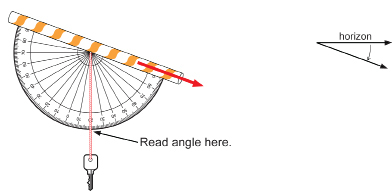
This illustration shows the clinometer pointing slightly downward to a distant object. The string is hanging straight down and an arrow points to the point the string crosses the protractor. The arrow is labelled read angle here.

 

Practise looking through the straw and measuring angles of elevation and depression. You will use your clinometer skills throughout this module.

 

TT 1. What is the largest angle of elevation you can measure? In practice, angles will be significantly less.

 

TT 2. What is the largest angle of depression you can measure? In practice, angles will be significantly less.

 

Keep this clinometer somewhere safe, since you will need it in the next lesson.

 

Skill with Ratios

 

An important algebra skill you will use repeatedly throughout this module involves equal ratios. You will now review how to determine if ratios are equal.

 

Example 1

 

Are and equal ratios?

 

Solution

 

Method 1: Reduce each fraction (ratio) to its simplest terms.

 

 

 

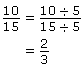
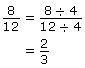
Since each ratio reduces to , the ratios are equal.

 

Method 2: Compare the cross products.

 

 

 

 

10 × 12 = 120

 

 

15 × 8 = 120

 

Because the cross products are equal, the ratios are equal.

 

The Principle

 

The previous example illustrates the following principle in algebra.

 

 

 

 

 

Self-Check

 

In each of the following questions, use both methods from the example to compare each pair of ratios.

 

SC 1. Are equal ratios?

 

SC 2. Are equal ratios?

 

Compare your answers.