1. Module 7

1.9. Page 4

Mathematics 10-3 Module 7 Lesson 2

Module 7: Trigonometry

 

Bringing Ideas Together

 

indirect measurement: taking one measurement in order to calculate another measurement

In the Explore section you explored indirect measurement using the tangent ratio. This means you used one measurement (the angle of elevation) to find another measurement (the height of the object). You used the following relationship to find the height of the object you selected.

 

 

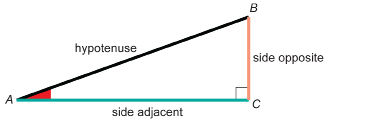
This illustration shows a right triangle ABC with angle A marked in red and angle C marked with a square. Side AC is labelled side adjacent and is aqua, side BC is labelled side opposite and is orange, and side AB is labelled hypotenuse and is black.

 

 

 

This relationship can be used, as it was in Explore, to find the side opposite. The relationship can also be used to determine the adjacent side or the reference acute angle in problem situations. Study the following examples to see how the tangent ratio can be used in a variety of ways.

 

Example 2

 

From a school window 5 m above the ground, a student measures the angle of depression to a fire hydrant located across the schoolyard. If the angle of depression is 10°, how far is the fire hydrant from the school? Round to the nearest metre.

 

Solution

 

Draw a diagram.

 

 

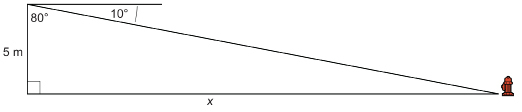
This illustration shows a right triangle with a horizontal leg extending from the wall of the school to the fire hydrant. The height of the triangle is 5 metres, and the base has measure x. A line parallel to the base is drawn from the upper vertex. The angle between this parallel line and the hypotenuse drawn from the upper vertex to the fire hydrant is 10 degrees. The interior angle at the upper vertex measures 80 degrees.

 

Method 1: Use the adjacent angle.

 

The angle of depression is the angle through which the observer must look down from the horizontal to see an object below. The angle adjacent to it in the right triangle is 80°, since the two angles must add up to 90°.

 

Substitute into the formula.

 

 

 

The fire hydrant is approximately 28 m from the school.

 

Method 2: Use the angle of elevation at the fire hydrant.

 

 

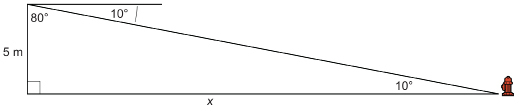
A right triangle is shown with the horizontal base extending from the wall of the school to the fire hydrant. The height of the triangle is 5 metres, and the base has measure x. A line parallel to the base is drawn from the upper vertex. The angle between this parallel line and the line drawn from the upper vertex to the fire hydrant is 10 degrees. The interior angle at the upper vertex measures 80 degrees. The third angle of the triangle is labelled 10 degrees.

 

The angle of elevation and the angle of depression are always equal because they are alternate interior angles.

 

Use the 10° angle as the reference angle. This time, the 5-m side is the side opposite.

 

Substitute into the formula.

 

 

 

 

This illustration shows the buttons on a calculator. The following button order is shown; 5, division sign, tan, one, zero, closing bracket, and equals sign.

 

Example 3

 

A flagpole casts a shadow 12 m long when the angle of elevation of the sun is 40°. How tall is the flagpole? Round to the nearest tenth.

 

View the animated “Flagpole Solution.”

 

Example 4

 

This is a photo of a teepee in southern Alberta.

© V. J. Matthew/shutterstock

A teepee at Head-Smashed-In Buffalo Jump is 14 ft high and 16 ft in diameter. What angle does the conical surface of the teepee make with the ground? Round to the nearest degree.

 

Solution

 

Draw a diagram of the side view of the teepee.

 

 

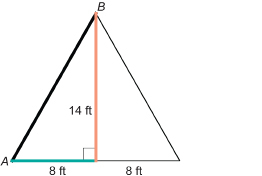
This illustration shows an isosceles triangle with a height of 14 feet. A line from the top vertex is drawn perpendicular to the base. This line bisects the base into two 8-foot segments. The right vertex of the base is labelled A.

 

Let ∠A be the required angle. The side view of the teepee is made up of two right triangles. The base of each right triangle is 8 ft long, since 8 ft + 8 ft = 16 ft, the diameter of the tent.

 

Substitute into the formula.

 

 

 

The side of the teepee makes a 60° angle with the ground.

 

It is your turn!

 

Self-Check

 

Apply the tangent ratios to find unknown sides and angles.

 

SC 3. A helicopter ambulance is dispatched from the airport to an accident scene 20 km north and 5 km east. What course should the helicopter fly to reach the accident scene directly?

 

SC 4. An airplane flying at an altitude of 1000 m is headed towards the North Battleford airport. If the angle of depression is 3°, how far, to the nearest 100 m measured along the ground, is the plane from the airport?

 

SC 5. Maxine is building a set of stairs with a -in riser and a 10-in tread. To the nearest tenth of a degree, what is the staircase angle? Regulations specify that the angle should not be more than 42°. Is Maxine within specifications?

 

SC 6. A ship’s navigator sights a lighthouse on the top of a vertical cliff. The light on the top of the lighthouse is 50 m above the sea. The navigator measures the angle of elevation of the light to be 1.5°. If the navigator’s charts say to stay at least 2 km from the foot of the cliff, is the ship safe?

This is an image of a sign that indicates a 10% grade.

© Bersanelli/12789445/Fotolia

 

SC 7. A sign on a hill warns truckers to test their brakes because the slope is 10%. A slope of 10% means that the road rises 10 m for a horizontal distance of 100 m. To the nearest degree, what angle is the road surface inclined to the horizontal?

 

SC 8. An airplane takes off from a runway and climbs at a 3° angle to the horizontal. If it maintains this rate of climb, what is the plane’s altitude above the ground to the nearest 100 m when the aircraft is 30 km away, measured along the ground, from the point it took off?

 

Compare your answers.

 

Mastering Concepts

 

This is a photo of the pyramid of Khafre and the Great Sphinx of Giza.

© ARCHITECTE®/shutterstock

The pyramid of Khafre and the other pyramids at Giza, near Cairo, have stood for over 4500 years as monuments to the genius of the ancient Egyptians. For centuries, these pyramids were the tallest human-made structures on the planet. Did you know that if you were to slice the Khafre pyramid in half vertically from the apex at the top to the base, the triangular cross-section is two 3-4-5 right triangles?

 

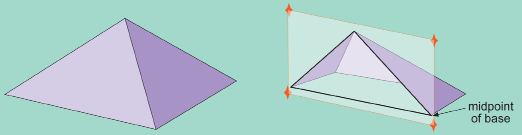
This illustration shows a pyramid with a square base and a cutaway of the same pyramid. The cutaway shows the pyramid cut through the middle of the base. The edge is highlighted in black and is in the shape of a triangle.

 

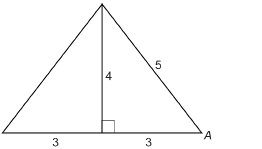
This illustration shows an isosceles triangle with a perpendicular bisector. The equal sides of the triangle are of length five units, the height of the triangle is four units, and the bases of the created right triangles are three units in length.

 

You will recall that the 3-4-5 right triangle was used by Egyptian surveyors. Do you remember the significance of these numbers? These numbers form a phythagorean triple and indicate a right triangle.

 

Determine ∠A to the nearest degree of the slant side of the Khafre pyramid.

 

Compare your answer.