Module 7
1. Module 7
1.15. Page 5
Module 7: Trigonometry
The Sine Ratio
Look at the table of sine ratios you prepared. What do you notice about the value of the sine ratio? What happens to the sine ratio as you move from an angle of 0° to 80°?
You should remember two benchmarks: sin 30° = 0.50, and sin 45° = 0.71.
These benchmarks, or referents, will help you assess whether or not an answer is reasonable!
Did You Know?
People tend to think of mathematics as a modern way of looking at the world. Did you know that the ancient Babylonians, Egyptians, Indians, and Greeks used trigonometric tables, especially in astronomy? The word sine, in fact, is a mistranslation into Latin. The word sinus means “bay,” which is what the translators thought the Arabic word written as jb meant. In fact, jb was simply borrowed from the Sanscrit (Indian) word jya-ardha, which means “half chord.” Indian mathematicians from more than 1500 years ago calculated tables of sines from half chords of circles correct to 4 decimal places!
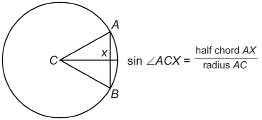
A chord is a line segment joining two points on a circle. Segment AB is a chord, and segment AX is a half chord. The ![]() . Fortunately, you don’t have to calculate sines using half chords as early mathematicians did. You can use a calculator!
. Fortunately, you don’t have to calculate sines using half chords as early mathematicians did. You can use a calculator!
Example 4
Find each sine, correct to 4 decimal places, using your calculator.
- sin 45°
- sin 30°
Solution
There are several different ways angles may be expressed. Make sure your calculator is set to degree mode.
- To find sin 45°, press this sequence of keys. If you don’t obtain the answer shown, consult your manual.

Your calculator should display something similar to what follows.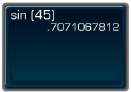
So, sin 30° 0.7071.
0.7071.
- To find sin 30°, press this sequence of keys. If you don’t obtain the answer shown, consult your manual.

Your calculator should display something similar to what follows.
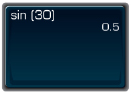
So, sin 30° = 0.5.
 Self-Check
Self-Check
Use the calculator method of the previous examples to complete the following table.
SC 6. Complete the following table. Round to 4 decimal places.
|
Angle |
Sine |
|
10° |
|
|
20° |
|
|
30° |
0.5000 |
|
40° |
|
|
45° |
|
|
50° |
|
|
60° |
|
|
70° |
|
|
80° |
|