Module 7
1. Module 7
1.16. Page 6
Module 7: Trigonometry
Solving Problems Using the Sine Ratio
In the next example you will apply your calculator skills to help you solve a problem involving the sine ratio.

iStockphoto/Thinkstock
Example 5
The photograph is of a mountain slope that often has avalanches.
Avalanches are triggered by human activity, such as snowmobiling, and most commonly occur on slopes between 35° and 45°.
Suppose the slope of a mountain slope is 38°, and the slope passes through a height of 800 m. What is the slope’s length? Round your answer to the nearest 100 m.
Solution
Draw a diagram.
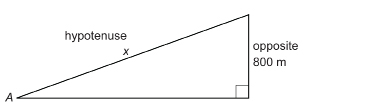
Let x be the length of the slope.
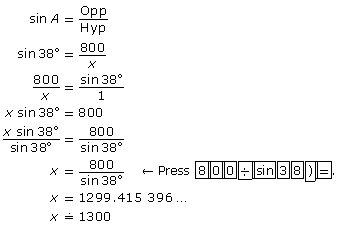
The mountain slope would be approximately 1300 m in length.
 Self-Check
Self-Check
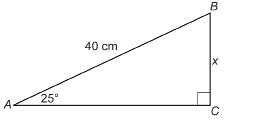
Use the method outlined in Example 5 to solve this question.
SC 7. Solve for x. Round to two decimal places.
Finding Angles Using the Sine Ratio
You have just seen how an unknown side in a right triangle can be determined using the sine ratio, provided you know the measure of an acute angle in that triangle. Can you find an angle using the sine ratio?
For instance, suppose you are told that the sine of a given acute angle in a right triangle is 0.6. What is the angle?
Example 6
If sin A = 0.6, determine ∠A to the nearest degree.
View the animated “Sine Solution.”
 Self-Check
Self-Check
Practise finding angles given the sine ratio.
SC 8. Find ∠A given sin A = 0.8.
Use both methods as shown in Example 6 to find the angle.
SC 9. Use your calculator to find each angle from its sine. Round your answers to the nearest tenth.
sin A |
∠A |
0.1257 |
|
0.7826 |
|
0.9000 |
|
|
|
|
|
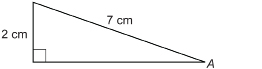
SC 10. Find ∠A to the nearest tenth of a degree.
 Mastering Concepts
Mastering Concepts
Try these questions. When you are finished, check your answer.
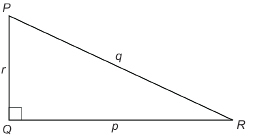
- For ΔPQR, write the ratios for sin P and sin R.
- How are ∠P and ∠R related?
- How are p and r related?