1. Lesson 2

1.12. Lesson 2 Summary

Mathematics 20-2 M3 Lesson 2

Module 3: Quadratics

 

Lesson 2 Summary

 

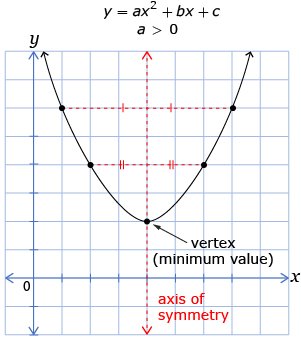
This shows a graph. The parabola opens upwards with a vertex above the x-axis. This parabola has a minimum value and no x-intercepts. The axis of symmetry is shown as an equal distance from points with the same y-values.

from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 332. Reproduced by permission.

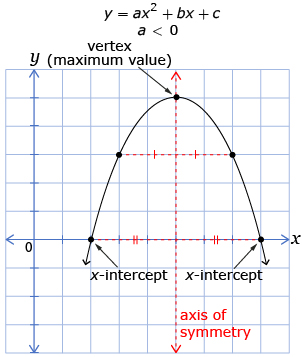
This shows a graph. The other parabola opens downwards with its vertex above the x-axis. It has a maximum value and two x-intercepts. The axis of symmetry is shown as an equal distance from points with the same y-values.

from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 332. Reproduced by permission.



In this lesson you found that the coordinates of the vertex of the parabola are for the point of maximum or minimum value of the quadratic function. The coordinates of this point can be determined from the graph. The axis of symmetry is the x-value of the vertex.

 

The domain will be all values of x that are possible for the function. It is symbolically written as 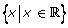when it includes all real numbers. The range is all the values of y that are possible for the function. It is symbolically written as 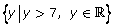when it includes all real numbers greater than 7, for example. When determining domain and range, it is important to consider the situation that is being modelled. Is it possible for a value to be below zero?

 

If the value of a is positive, the graph will open upwards. If the value of a is negative, the graph will open downwards. In each case, the position of the vertex will determine whether there are two, one, or zero x-intercepts.

 

If a is positive, the graph opens upwards and the following statements are true:

  • If the vertex is below the x-axis, there will be two x-intercepts because both arms of the parabola will cross the x-axis.

  • If the vertex is on the x-axis, there will be one x-intercept because the parabola touches the x-axis at one point.

  • If the vertex is above the x-axis, there will be zero x-intercepts because the parabola will never cross the x-axis.

If a is negative, the graph opens downwards and the following statements are true:

  • If the vertex is below the x-axis, there will be zero x-intercepts because the parabola will never cross the x-axis.

  • If the vertex is on the x-axis, there will be one x-intercept because the parabola touches the x-axis at one point.

  • If the vertex is above the x-axis, there will be two x-intercepts because both arms of the parabola will cross the x-axis.

In Lesson 3 you will investigate how to use a graphing technology to find the maximum or minimum value, the axis of symmetry, the x- and y-intercepts, and the coordinates of the vertex.