Lesson 1

In Try This 2 you probably discovered that x-intercepts are directly related to the factors of a polynomial function. The following example illustrates the relationship between a polynomial function and the x-intercepts of its graph.

 

What are the x-intercepts of the graph of f(x) = 0.4(x − 3)(x + 5)(x − 1)?

 

You need two key pieces of information:

• All x-intercepts have y-coordinates of zero.
  
• The zero-product property: If s and t are real numbers and st = 0, then either s must be zero, t must be zero, or they are both zero. (This can be extended to the product of any number of numbers.)

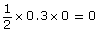
Since the x-intercepts have y-coordinates of zero, you are looking for values that make the following equation true:

 

0.4(x − 3)(x + 5)(x − 1) = 0

 

The left side is the product of four real numbers: 0.4, x − 3, x + 5, and x − 1. The only way a product of numbers can be zero is if one (or more) of those numbers is zero (the zero-product property). Thus,

 

0.4 = 0 (1)

 

x − 3 = 0 (2)

 

x + 5 = 0 (3)

 

x − 1 = 0 (4)

 

Equation (1) is false, so it can be ignored. Solving the other three equations gives three values of x that make the original equation true:

 

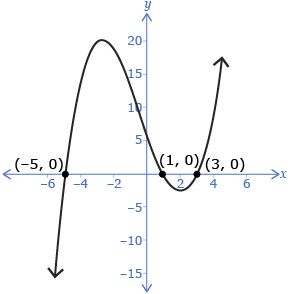
x = 3

 

x = −5

 

x = 1

 

These make the polynomial function zero, so they are the x-intercepts. Graphing the polynomial function confirms this.

 

 

Self-Check 3

 

State the x-intercepts of the graphs of the following functions without graphing them.

1. f(x) = (x − 1)(x + 3)(x + 7) Answer
2. k(x) = −3(x + 2)(x − 3)(x − 6) Answer
3. Answer
4. f(x) = x2 − 3x − 4 Answer