1. Lesson 1

1.10. Explore 6

Mathematics 30-1 Module 3

Module 3: Polynomial Functions

 

In Try This 3 you may have discovered that the number of times a factor is duplicated affects the graph’s behaviour around the corresponding x-intercept.

  • If a factor is repeated an odd number of times, the function changes sign (the graph crosses the x-axis) at the corresponding x-intercept.
  • If a factor is repeated an even number of times, the function does not change sign (the graph touches but does not cross the x-axis) at the corresponding x-intercept.

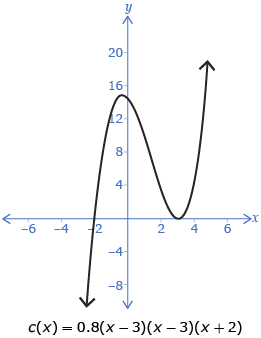
Consider the function c(x) = 0.8(x − 3)(x − 3)(x + 2). The factor x + 2 is repeated an odd number of times, so the function changes sign at the corresponding x-intercept (x = −2). The factor x − 3 is repeated an even number of times, so the function does not change signs at the corresponding x-intercept (x = 3).

 

Mathematicians would say that the factor x − 3 has a multiplicity of 2 and that the factor x + 2 has a multiplicity of 1.

 

This shows the graph of c(x) = 0.8(x – 3)(x – 3)(x + 2). This graph crosses the x-axis at (0, –2) and touches it at (0, 3).



textbook

Read “Example 1” on pages 138 and 139 of the textbook for two more examples concerning multiplicity of factors and x-intercepts. Pay particular attention to

  • “multiplicity (of a zero)” in the left column (Notice how the graph “flattens” near an x-intercept of multiplicity 3.)
  • the analysis of the least possible degree of the polynomial