1. Lesson 3

1.11. Lesson 3 Summary

Mathematics 30-1 Module 2

Module 2: Radical Functions

 

Lesson 3 Summary

 

In this lesson you explored solving radical equations graphically. The solutions, or roots, of a radical equation are equivalent to the x-intercepts of the corresponding radical function. Two graphical methods were discussed.

 

Using a single function:

  • Rearrange the equation so that one side is equal to zero, and then graph the function. The solution is found by determining the value of the x-intercept(s).
  • The solution of the equation 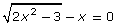is x ≈ 1.73.

     
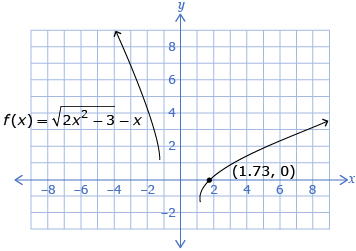
    This shows a graph with two curved lines of the function y equals square root 2 times x squared subtract 3 end square root, subtract x is shown with the x-intercept (1.73, 0) labelled.

  • The solution for the equation is 1.73.

Using a system of two functions:

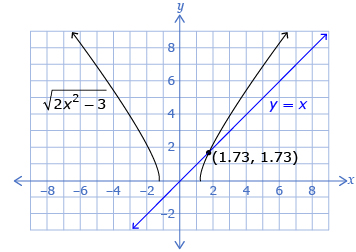
  • Graph each side of the equation as two separate functions. The solution is determined by the value of x at the point(s) of intersection.
  • The solution of the equation is x ≈ 1.73.

     
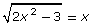    This is a graph of two functions. One function has two curved lines and is y equals square root of 2 times x squared subtract three. The other function is a straight line and is y equals x. The intersection point between the two functions is labelled (1.73, 1.73).

Radical equations that are used in various contexts, such as accelerated motion, can be solved using a graphical method.