Lesson 1
1. Lesson 1
1.5. Discover 2
Module 5: Radicals
Kenton decides to go visit his brother, Darius, and roommate, Troy, for the weekend. To pay them back for letting him stay at their place, Kenton agrees to wait for their new wall unit to be delivered for their living room and let the delivery people know where it needs to be set up.
Troy is in college and not only does he love math but he enjoys playing practical jokes on people. The directions Troy leaves state that the wall unit is ![]() m long and the dimensions of the living room are 9 ft wide by 11 ft long. Kenton needs to figure out which wall of the living room will be used to set up the wall unit.
m long and the dimensions of the living room are 9 ft wide by 11 ft long. Kenton needs to figure out which wall of the living room will be used to set up the wall unit.
Given the shape of the room and hallways, the delivery workers will have to use the front door if the wall unit will be on an 11-ft wall or the back door if the wall unit will be on a 9-ft wall.
By the end of this lesson, you’ll be able to answer this question using your knowledge of entire and mixed radicals.
Converting an entire radical into a mixed radical is the same as writing a radical in its simplest form. A simple method of doing this is to begin by determining the prime factors of the number. This can be done using a factor tree.
Look at Factor Tree to see example factor trees for the number 30. Notice how the factor tree can be created many different ways, but it always results in the same prime factors: 2, 3, and 5.
Try This 1
In this activity, you will return to Factor Tree and use the demonstration applet to rewrite radicands as products of prime factors. Scroll down the website until you come to “Demonstration Applet.”
Using the demonstration applet, you will complete the Radical Expression Chart.
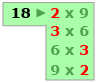
For each radical expression provided in the chart, perform the following steps. The first radical expression on the chart, 18, is done as an example.
Step 1: Enter the radicand (e.g., 18) in the grey box at the top of the applet. Then press enter.
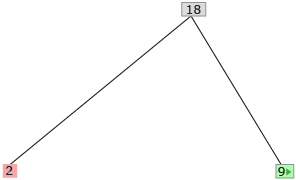
Step 2: Click on the green box that appears.
Step 3: Click on the first factored expression that appears.
Step 4: A pink box and a green box appear. The pink box is a prime number, and the green box is not. Click on the green box again, and select the first factored expression that appears.
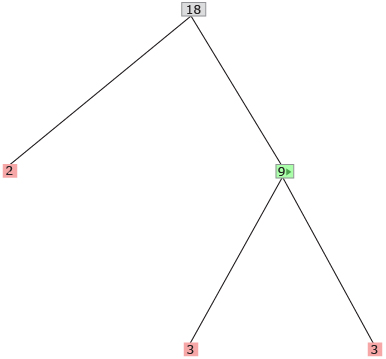
Continue this process until only pink boxes are displayed. These are the prime factors of the original number that you entered into the applet. Rewrite the radical expression with a factored radicand in the chart.
You can use prime factorization to change an entire radical into a mixed radical. Recall that perfect squares are found when multiplying a number by itself; for example, 2 × 2 = 4 and 3 × 3 = 9. It is easy to find the square root of a perfect square:
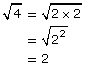 |
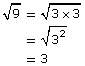 |
By writing the prime factorization as powers, the factors with even exponents can be found quickly and their square roots identified.
When dealing with cube roots, the factors that appear multiples of 3 times can be found quickly and their cube roots identified.
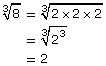 |
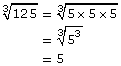 |
principal square root: the positive square root of a number
For example, the principal square root of 4 is 2.
secondary square root: the negative square root of a number
For example, the secondary square root of 4 is −2.
It is important to remember that there are principal square roots (positive) and secondary square roots (negative). Unless you are asked for both the principal and secondary square roots, the square root sign refers to the principal square root of an expression.
The next activity will help you discover what rules apply when multiplying radicals. This will help you when converting between mixed and entire radicals.