Lesson 1
1. Lesson 1
1.5. Explore
Module 4: Foundations of Trigonometry
Explore
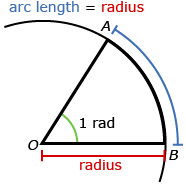
In Try This 1 you created a central angle where the radius, AO, of the circle is the same as the length of the subtended arc, AB. This situation defines radian measure. The measure of ∠AOB is 1 rad (radian).
You may have determined that the radius of the circle would fit about 6 times around the circumference of a circle. This would mean that one full rotation, which is 360°, would be the same as about 6 rad. In Try This 2 you will try to find a more precise value for one full rotation of a circle measured in radians.
Try This 2
You will test your new understanding of 1 rad by investigating whether the radius of a circle changes the measure of the central angle. You will then explore the relationship between radians and degrees.
Step 1: Open Angles in Degrees and Radians.
Step 2: Slide the angle slider to change the angle to 60°. Use the arrow keys on your keyboard to change the angle by 1° at a time. Note where 1 rad is positioned.
Step 3: Slide the radius slider to change the radius to a larger value and then to a smaller value. Did the radian measure change? Why do you think this happens? ![]()
- Use Angles in Degrees and Radians to complete a chart similar to the one that follows. You will notice that the radian measure is given in red as an exact measure in terms of π first and is then rounded to three decimal places.
Degree Portion of Whole Circle Radian Measure
(in terms of π)
Radian Measure
(round to three decimal places)
Sketch or Screen Capture 360° 1 
180° 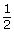

90° 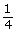

45° 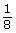

−360° −1 
−180° 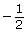

−90° 

−45° 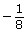

- If the angle is positive, in which direction does the terminal arm rotate?

-
If the angle is negative, in which direction does the terminal arm rotate?

- What relationship can you see between degrees and radians? Describe this relationship in terms of π rad.
Use the relationship you found in question 4 to answer the following questions.
- How are degrees related to radians?
- Complete a chart similar to the one that follows. Leave radians as exact measures. You can check your answers when you are finished by using Angles in Degrees and Radians.
Degree Radian
(exact value, fraction of π)
Sketch Quadrant 30° 
60° 
−120° 
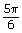

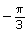

![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or in a group, discuss the following questions:
- How did you determine the answer to questions 5 and 6?
- Are your methods for changing degrees to radians and radians to degrees the same or different than your partner’s methods?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.