1. Lesson 5

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

Lesson 5: Trigonometric Equations

 

Focus

 

This photo shows a Formula 1 race car as it is being driven along a track.

iStockphoto/Thinkstock

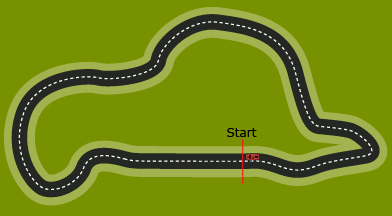
The Circuit Gilles Villeneuve is a motor-racing circuit in Montréal that hosts the Canadian Grand Prix car race. During this Formula 1 race, cars reach speeds of 360 km/h while traveling 70 laps around the 4.4-km loop.

 

Suppose you wanted to answer this question: How far has a car travelled when it crosses the finish line? You might answer 4.4 km, 8.8 km, or something else. How many answers are there? Is there a way to represent all of these answers without writing each one out?



In this lesson you will learn to solve some first- and second-degree trigonometric equations. You will also learn how to represent an infinite number of solutions as a general solution.

 

This diagram shows a race track with the starting line marked.

 

Lesson Outcomes

 

At the end of this lesson you will be able to

  • determine the measure of angles that produce a given trigonometric ratio
  • algebraically determine the solution to a first- and second-degree trigonometric equation over a restricted domain
  • verify a solution to a trigonometric equation
  • determine a general solution to a trigonometric equation
  • solve problems using trigonometric ratios
Lesson Questions

 

You will investigate the following questions:

  • How can trigonometric equations be solved?
  • How is a specific solution for a trigonometric equation related to the general solution?
Assessment

 

Your assessment may be based on a combination of the following tasks:

  • completion of the Lesson 5 Assignment (Download the Lesson 5 Assignment and save it in your course folder now.)
  • course folder submissions from Try This and Share activities
  • additions to Glossary Terms
  • work under Project Connection