Lesson 7
1. Lesson 7
1.3. Explore 3
Module 5: Radicals
Hemera/Thinkstock
In the early 1600s, Galileo discovered that the swinging motion of a pendulum does not change even if the width of the swing changed or the weight at the bottom of the pendulum changed. He found that it was the length of the pendulum that determined its period of motion.
Self-Check 1
- Galileo discovered that the time for a complete back-and-forth swing of a pendulum (called one period) is directly proportional to the square root of the length and inversely proportional to the square root of the acceleration due to gravity. The constant of proportionality is 2π. Another way of saying this is that the period is 2π times the square root of the pendulum length divided by the square root of acceleration due to gravity.
- Write an equation expressing the relationship between the period T of a pendulum and its length. Use L for length and g for the acceleration due to gravity. Notice how the variables are chosen to indicate what each represents. State any restrictions on the variables.
- A pendulum in a wall clock has a length of 1.4 m. What is the period of that pendulum to the nearest hundredth of a second if the acceleration due to gravity is 9.81 m/s2?
- Find the length of a pendulum that will give a period of 2 s. This means that the clock will tick precisely every second, at each end of the
back-and-forth swing of the pendulum.
- Write an equation expressing the relationship between the period T of a pendulum and its length. Use L for length and g for the acceleration due to gravity. Notice how the variables are chosen to indicate what each represents. State any restrictions on the variables.
-
The power in watts (W) of a hair dryer is equal to the ratio of the current in amps (A) squared multiplied by the resistance in ohms (Ω).
Christopher Robbins/Photodisc/Thinkstock- Express the statement as an equation, where power is P, current is I, and resistance is R.
- Rearrange the equation to isolate current, I.
- How much current flows through a 1600-W hair dryer that has a resistance of 8.82 ohms?
iStockphoto/Thinkstock
- Express the statement as an equation, where power is P, current is I, and resistance is R.
- Most new TV screens have a 16:9 aspect ratio. This means the width is
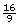times the height. When a television is advertised as having a 42-in screen, it means the length of the diagonal of the screen is 42 in.-
Determine the height of a 42-in screen. Begin by letting the height be h. Then express the width in terms of height. In your answer, include a
- description of any restrictions on the variables
- drawing using your variables and putting in the length of the diagonal
- description of any restrictions on the variables
Use the Pythagorean theorem to set up an equation and solve for the height.
Is your answer reasonable?
- Determine the width of a 42-in screen. How can you check your answer?
- What is the total viewing area of a 42-in screen?
-
Determine the height of a 42-in screen. Begin by letting the height be h. Then express the width in terms of height. In your answer, include a
- Complete “Practising” questions 11, 12, 13, and 14 on pages 223 and 224 of your textbook.
Answer
Read “Frequently Asked Questions” on pages 226 and 227 of your textbook. If you have any additional questions about solving problems with radical equations, be sure to contact your teacher.
If you have not already done so, now would be a good time to add important concepts to your notes organizer that you have saved to your course folder.