Lesson 1

Refresher

 

Recall that a ratio is a comparison of numbers or quantities. For example, the ratio of red marbles to blue marbles in the following diagram could be expressed in the following ways:

 

• 2 to 4
• 2:4
• 

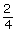
The ratio 2:4 can be written in lowest terms as 1:2. The ratio 2:4 is said to be equivalent to the ratio 1:2. In other words, 2:4 = 1:2. Equivalent ratios can be written in any of the forms that ratios can be written.

• 1:2
• 1 to 2
• 

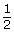
A ratio can compare numbers with the same or different units. Consider the following three plates. Each plate has four slices of pizza on it.

 

 

The ratio of slices of pizza to plates could be expressed as

• 12 to 3
• 12:3
• 

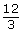
The ratio of slices of pizza to plates could also be expressed in lowest terms as 4:1.

 

These ratios have different units for each part of the ratio. Here the ratio represents the number of slices of pizza to the number of plates (4 slices of pizza to 1 plate).

 

A proportion is made up of two or more ratios that are equivalent.

 

 

Proportions can be used to solve for unknown values. For example, you could use the ratio of the 12 slices of pizza to 3 plates to set up a proportion to determine how many slices of pizza (p) would be on 20 plates if the pizza was arranged the same on all 20 plates.

 

Begin by writing a proportion with the unknown value represented by a variable. Use p to represent the pizza slices.

 

 

To find the number of slices of pizza, you need to isolate the variable, p.

 

 

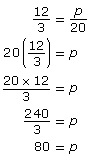
There are 80 slices of pizza on 20 plates.

 

For more information on proportion and how ratios can be used to solve problems, refer to the Proportion definition.