Lesson 4
1. Lesson 4
1.3. Lesson 4 Summary
Module 6: Proportional Reasoning
Lesson 4 Summary
In this lesson you investigated how diagrams and models can be used to represent 2-D shapes and 3-D objects. These diagrams allow sculptors and designers to produce an accurate representation of what their designs would look like on larger-than-life canvases, like a mountain, or smaller canvases, such as a coffee mug.
Scale models are proportional representations of 3-D objects. Scale diagrams are proportional representations of 2-D shapes. Designers use scale to produce accurate and proportional representations of objects and shapes. By relating the diagram or model’s measurement to the actual measurement, the scale factor can be determined.
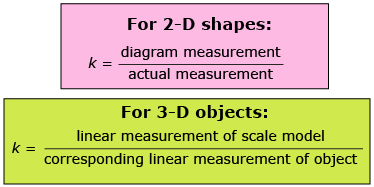
A scale factor of greater than 1 will result in an enlargement, while a scale factor between 0 and 1 results in a reduction. A scale factor of exactly 1 represents a full scale (1:1) model, which means that the dimensions stay the same.
In order for a diagram to be proportional to the original, all items on the diagram have to be drawn to the same scale. Likewise, in order for a model to be proportional to the original shape, all linear measurements need to be related by the same scale factor.
In Lesson 5 you will use scale diagrams and models to determine unknown dimensions.