1. Module 6

1.19. Page 4

Mathematics 10-3 Module 6: Lesson 4

Module 6: Triangles and Other Polygons

 

Bringing Ideas Together

 

In the Explore section you investigated a practical problem involving similar right triangles. Remember, two right triangles are similar if there is a pair of congruent, corresponding acute angles.

 

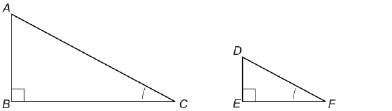
This illustration shows right triangles ABC and DEF. Angles B and E are right angles, and angles C and F are each marked with a single arc.

 

ΔABC is similar to ΔDEF since ∠C is congruent to ∠F.

 

For a reminder on how to use and read symbols, listen to “” and “”



Of course, not all similar triangles are right triangles. In the previous lesson, you explored the following requirements, or conditions, for stating that any pair of triangles are similar:

  • The corresponding angles are congruent.

  • The corresponding sides are proportional.

  • One pair of angles is congruent and the two pairs of corresponding sides that form those angles are proportional.

The following examples and Self-Check questions involve identifying similar triangles in problem-solving contexts, and then applying proportional reasoning to solve these problems.

 

Example 1

 

This is a photograph of a Curtiss biplane.

Topical Press Agency/Hulton Archive/Getty Images

 

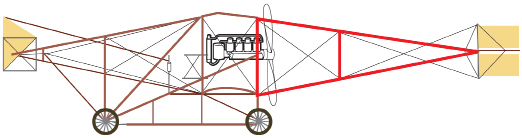
This is an illustration of a Curtiss biplane.

 

Petranella is building a scale model of a 1910 Curtiss biplane. She is working on the tail section and has taken measurements from an online graphic, but she forgot to measure x. What is the measure of x correct to one decimal place?

 

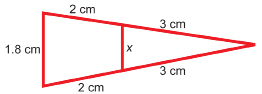
This illustration shows a large triangle with a segment joining two sides and creating a smaller triangle. This segment has length x. Each of the two sides x joins is divided into segments of length 2 and 3 centimetres. The third side of the large triangle measures 1.8 centimetres.

 

Solution

 

Separate the triangles. Are the triangles similar?

 

The two triangles share an angle at the tail section.

 

The ratios of the sides forming the shared angle are equal,

 

As a pair of angles is congruent and the two pairs of corresponding sides that form those angles are proportional, the triangles are similar.

 

Set up a proportion.

 

 

 

 

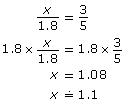
The missing measure is approximately 1.1 cm.

 

Example 2

 

This is a photograph of a woman in a wheelchair descending a ramp.

© prism68/shutterstock

A wheelchair ramp is 5 m in length. The bottom of the ramp is 0.6 m below the top of the ramp. When a wheelchair is moved 2 m down the ramp, how far is the wheelchair above the foot of the ramp?

 

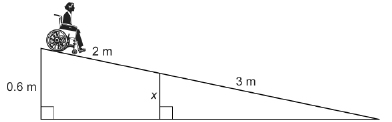
This illustration shows a right triangle with a horizontal base. The right angle is at the left of the triangle. The vertical side measures 0.6 metres. The hypotenuse is split into two parts measuring 2 metres and 3 metres. The line causing the split is x high and forms a right angle with the base of the triangle.

 

Solution

 

Separate the triangles.

 

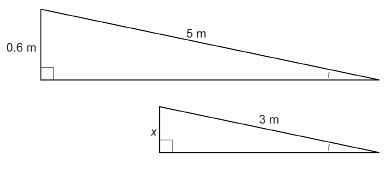
This illustration shows two right triangles. The larger triangle has a hypotenuse that measures 5 metres, a small angle marked with a single arc, and the side opposite the marked angle that measures 0.6 metres. The smaller triangle has a hypotenuse that measures 3 metres, a small angle marked with a single arc, and the side opposite the marked angle that measures x.

 

Are the triangles similar?

 

Observe that the two right triangles share an acute angle. So, you can apply Condition 4 for congruence of right triangles.

 

You may remember Condition 4 from the following diagram.

 

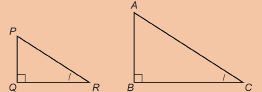
This illustration shows two right triangles, PQR and ABC. Angles Q and B are right angles, and angles R and C are each marked with a single arc.

 

Condition 4: For right triangles, if one pair of acute angles is equal in measure, the triangles are similar.



In the separated triangles describing the ramp, the marked angles are acute and congruent. So, Condition 4 is met. Therefore, these right triangles are similar, and the ratios of the corresponding sides of these right triangles are proportional.

 

Set up a proportion.

 

 

 

 

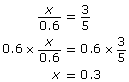
The wheelchair is 0.36 m above the foot of the ramp.

 

Self-Check

 

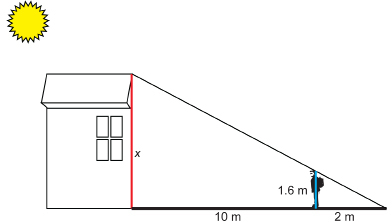
SC 4. Jon walked 10 m away from a wall outside of his school. At that point, he noticed that his shadow reached the same point on the ground as the school’s shadow. If Jon is 1.6 m tall and his shadow is 2 m long, how high is the school? Round to one decimal place.

 

This illustration shows a right triangle with a red vertical side that measures x. A blue vertical line drops from the hypotenuse and divides the horizontal base into a 10-metre segment and a 2-metre segment. The blue vertical segment measures 1.6 metres. The school is next to the red vertical side of the triangle, and a student is located at the blue vertical line. The Sun, in the upper left of the diagram, is lined up with the hypotenuse of the right triangle.

 

SC 5. Dace is standing on the shore of the North Saskatchewan River. She sees a fisherman, F, on the opposite bank.

 

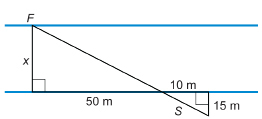
This illustration shows two parallel, blue, horizontal lines that are x metres apart. A point, F, is on the top parallel line. A point, S, is on the bottom parallel line. A line segment is drawn from F directly across the river—perpendicular to the parallel lines. A line is drawn 60 metres along the bottom parallel line. Point S is marked on this line 50 metres from the point across from F. A line perpendicular to the bottom parallel line is drawn away from the river. This line measures 15 metres. A line from this point through S is extended and meets point F.

 

She would like to know how wide the river is at this point. Dace walks 50 m downstream along the riverbank. She stops and pushes a stick, S, into the bank. Dace walks another 10 m downstream, and then turns 90°. She now walks 15 m away from the river until she sees that the stick she pushed into the bank lines up with the fisherman across the river. Calculate the width, x, of the river.

 

SC 6. A chalet in the mountains has a triangular profile.

 

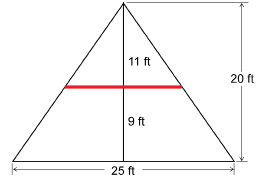
This illustration shows a triangle that is 20 feet tall and has a base that is 25 feet wide. A red line is drawn parallel to the base and 9 feet above the base.

 

There is a balcony 9 ft above the ground. If the chalet is 25 ft across the base and 20 ft high, what is the width of the balcony?

 

SC 7. The crossed legs of an ironing board are illustrated.

 

This picture shows and ironing board with a shirt on one end and an iron on the other. The two legs of the ironing board cross about one third of the distance from the horizontal ironing surface and the floor.

© Lane V. Erickson/shutterstock

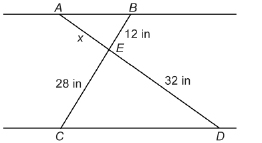
This illustration shows two parallel line segments and two crossing segments that join them. The top parallel line has points A and B as the starting points for the second pair of line segments AD and BC. AD and BC cross at point E. Segment AE measures x inches. Segment ED measures 32 inches. Segment BE measures 12 inches. Segment EC measures 28 inches.


 

  1. If the top of the ironing board is parallel to the floor, is ΔABE similar to ΔDCE? Justify your answer.

  2. Determine the value of x to the nearest tenth of an inch.

SC 8. A 2-m pry bar is placed under a timber 20 cm from the end of the bar. The free end of the bar is lifted 30 cm. How high off the ground is the timber?

 

This illustration shows a right triangle with a horizontal base and a vertical side that measures 30 centimetres. A red square sits on the hypotenuse 20 centimetres from the lower end. A vertical segment is shown dropping from the box’s position on the hypotenuse. This vertical segment measures x centimetres.

 

Compare your answers.

 

Mastering Concepts

 

Try this question. When you are finished, check your answer.

 

 

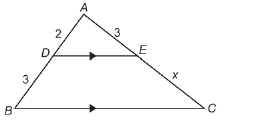
This illustration shows triangle ABC with horizontal base BC. Line segment DE is shown parallel to BC and joins segments AB and AC. D is a point on AB that is 2 units from A and 3 units from B. E is a point on AC that is 3 units from A and x units from C.

  1. Why are 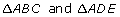similar?

  2. Determine the value of x.

Compare your answers.