Lesson 3

Explore

In Try This 1 you saw that y = cos θ and y = sin θ cot θ have the same values when both functions are defined. cos θ = sin θ cot θ is an example of a trigonometric identity. A trigonometric identity is a trigonometric equation that is true for all permissible values of the variable in the expressions on both sides of the equation.1

You have already experienced a number of trigonometric identities so far in this course, including reciprocal and quotient identities. Think of how they got their names.

It is often possible to predict whether a statement is an identity by verifying the statement numerically or graphically. Try This 2 explores this idea.

Try This 2

Consider the following equations:

1. Do you expect either of the equations to be a trigonometric identity? Explain.
2. Determine the non-permissible values for each equation.
3. Attempt to verify each potential identity by checking that both 40° and 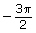are solutions.
4. If you were to plot 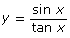and y = cos x on the same graph and then plot 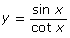and y = cos x on the same graph, which two graphs would you expect to overlap one another?
5. Plot the graphs in question 4 for domain −2π ≤ θ ≤ 2π. Was your prediction from question 4 correct?

Save your answers in your course folder.

Share 2

With a partner or group, discuss the following questions based on your answers from Try This 2.

1. Explain which of the two equations from Try This 2 you think is an identity.
2. Looking back at the definition for a trigonometric identity and using the information in Try This 2, is it possible to be sure the equation is an identity? Explain.

If required, save a record of your discussion in your course folder.

1 Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011. Reproduced with permission.