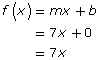Lesson 2

Arithmetic Sequences and Linear Functions

 

In Try This 1 you saw how investments earning simple interest follow an arithmetic progression that can be expressed in the form tn = a + (n − 1)d. You then represented this as a linear function.

 

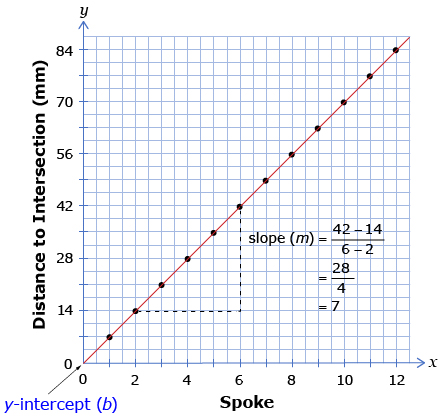
In the Math Lab, you investigated arithmetic progressions based on an Archimedes' Spiral. You may have discovered that the points of intersection with each spoke of the spiral follow an arithmetic progression that can also be expressed in the form tn = a + (n − 1)d. You then plotted a graph showing tn versus n. Retrieve this graph from your course folder. Compare your graph to Figure 1.

 

 

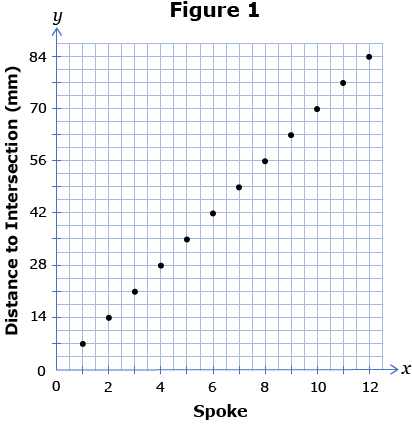
Your graph should also show 12 points positioned along a diagonal. Would it be more or less appropriate to sketch the graph as shown in Figure 2?

 

 

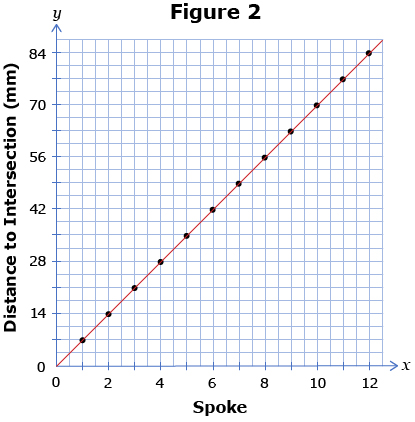
Notice that, in Figure 2, a line is drawn through the points. If a graph is drawn in this way, it is implied that every point on the graph is valid, even the points that occur between the points marked in black.

 

There are many points on the graph that do not have meaning in the context of Archimedes' Spiral. For example, the point (1.5, 10.5) is on the line but has no meaning in the context of the investigation, since there is no spoke between the first and second spoke!

 

 

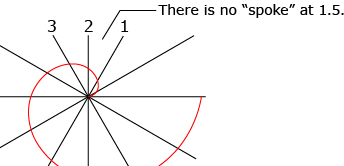
Recall from your previous math studies that the equation of a linear function is given by the form f(x) = mx + b. You can use this formula to determine the equation of the line representing the Archimedes' Spiral.