Lesson 3

Lesson 3 Summary

 

In this lesson you investigated the following questions:

• How are arithmetic sequences and arithmetic series similar and different?

• How can you visualize the sum of an arithmetic series?

You extended your understanding of arithmetic sequences to arithmetic series. An arithmetic series is the sum of the terms of an arithmetic sequence. Both arithmetic sequences and arithmetic series have the property that consecutive terms are related by a common difference.

 

In general, the general term tn = a + (n − 1)d is used to determine properties of an arithmetic sequence. The formulas  and  are used to determine the properties of an arithmetic series. In the case of the general term, the parameter n refers to the position of the term; in the series formulas, n refers to the number of terms that will be added together.

 

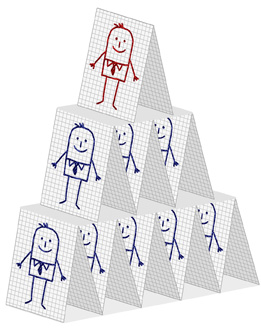
In this lesson you learned about Gauss’ method for evaluating an arithmetic series. You visualized Gauss’ method by placing two images of pyramids together. Later in the lesson you were able to build on that initial discovery to derive formulas that could be used to determine the sum of an arithmetic series.

 

You used the formulas to solve context-based problems. You practised using the formulas with and without rearranging. You learned to match given information within a problem with the variables of each problem. You discovered that there is more than one correct way to arrive at a solution.

 

You have now completed half of Module 1. In the second half of Module 1 you will explore a different kind of sequence—geometric. Geometric sequences and series can be used to describe a variety of different phenomenon, including population growth and radioactive decay. You will learn that these sequences have many applications in finance.