Lesson 5

Geometric Series and Investing

 

In the introduction to Explore you read that a 15-year-old who invests $200/mo for 10 yr will have earned more money by the time she is 65 years old than a 25-year old who invests $200/mo for 40 yr. You now have the mathematical know-how to be able to prove this statement.

 

The following example will show you the total value of the 15-year-old’s investment. Work through the example to see how the concepts of geometric series are used to determine the answer. Then use the same principles to determine the value of the 25-year-old’s investment.

 

Example

 

Ming, a 15-year-old, contributes $200/mo towards an investment that pays 9%/yr compounded monthly. She pays $200 at the beginning of every month for 10 yrs. She then stops contributing to the investment, allowing the investment to continue accumulating interest. Determine the total value of the investment when Ming is 65 years old.

 

Solution

 

Value to be Determined	Calculation	Reasoning
number of months in 10 yr	10 yr × 12 mo/yr = 120 mo	There are 120 mo in 10 yr.
interest rate per month	9% ÷ 12 = 0.75%	The monthly interest is 0.75%. For the purposes of calculations using the compound interest formula, you will use 0.0075 to represent i.
value of the 1st $200 contributed		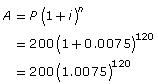The first $200 will earn interest for the full 10 yr, or 120 mo.
value of the 2nd $200 contributed	200(1 + 0.0075)119 = 200(1.0075)119	The second $200 will earn interest for the full 10 yr less 1 mo, or 119 mo altogether.
value of the 3rd $200 contributed	200(1 + 0.0075)118 = 200(1.0075)118	The third $200 will earn interest for the full 10 yr less 2 mo, or 118 mo altogether.

 

A geometric series can be formed, where the first three terms are:

 

200(1.0075)120 + 200(1.0075)119 + 200(1.0075)118 + + 200(1.0075)2 + 200(1.0075)1

 

Value to be Determined	Calculation	Reasoning
sum of the geometric series		The total value of the investment after 10 yr is $38 993.13.
amount of time the investment is allowed to earn interest after the initial 10 yr of contributions	65 − 25 = 40 yr 40 yr = 40 × 12 = 480 mo	Ming will be 25 years old when she pays her final $200 contribution. The investment will now gain interest for 40 more years until she is 65 years old.
value of the investment when Ming is 65		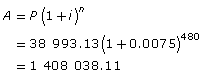Ming’s investment will be worth $1 408 038.11.