Lesson 6
1. Lesson 6
1.6. Explore 2
Module 1: Sequences and Series
What Is the Sum of an Infinite Number of Terms?
Think back to Lesson 5 Try This 1. In that activity you investigated a geometric pattern involving grains of rice on consecutive squares of a chessboard. You discovered that each time you advanced to the next square, the total number of grains of rice increases. Indeed, the sum of the series did not get close to any particular number—the sum only increased in size dramatically as more terms were added.
It would seem logical that as you add more terms to an existing sum, the resulting sum grows larger. As you continue to add even more terms, the result approaches infinity. Therefore, you can assume that the sum of an infinite number of terms is infinity. Despite this logic, however, Try This 1 in this lesson shows that this does not hold true in all cases.
Watch Discovering Infinite Trapezoids Video to see one way in which a student might have completed Try This 1. The video only shows the process of dividing and shading trapezoids a few times. Ask yourself what the diagram would look like if it were actually possible to shade an infinite number of trapezoids.
- How would you describe the shape of the shaded area?
- What fraction of the whole trapezoid would this shaded area represent?
You have seen in the video that the sum of an infinite number of terms can approach a finite number! It seems that as you add more area, the total area does not get closer to infinity; instead the total area approaches one-third.
A series whose sum approaches a finite number is said to be convergent. In contrast, a series whose sum does not approach any particular number is called divergent.
How do you know if a series will be convergent or divergent? In this Math Lab you will investigate the properties of series in order to identify them as convergent or divergent.
Materials
You will need a graphing calculator or graphing software.
Problem
How do you know if an infinite geometric series is convergent or divergent?
Procedure
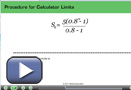
Watch Procedure for Calculator Limits to see how you should carry out the steps in this Math Lab. The procedure should be applied to each of the series given in the table.
Table
Complete a table like this one:
| Series | Standard Form | Common Ratio | Sn | Sum Limit |
| A | 2 + 6 + 18 + 54 + … | |||
| B | ||||
| C | 10 000 − 1000 + 100 − 10 + … | |||
| D | 0.6 − 4.2 + 29.4 − 205.8 + … |
Analysis
- Which series seemed to approach a number as the number of terms increased? Which ones did not approach any particular number?
- Review the pattern in the table. What property of a series can be used to separate geometric series that have a limit from geometric series that do not have a limit. Explain.