Lesson 6
1. Lesson 6
1.9. Explore 5
Module 1: Sequences and Series
Try This 3
Retrieve your results from Try This 1. Your task in that activity was to determine the fraction of the original trapezoid that was shaded. You can now use the formula for evaluating the sum of an infinite geometric series to confirm your answer to that activity.
- Represent the shaded areas with the first few terms of an infinite series.
- Use the expression
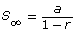 to evaluate the total shaded area. Does the answer confirm the result you obtained in Try This 1?
to evaluate the total shaded area. Does the answer confirm the result you obtained in Try This 1?
If your results do not match, return to your work in Try This 1. Retrace the steps you followed to determine the shaded area. You can try counting the number of grid triangles. Then divide this number by the total number of grid triangles in the original trapezoid.
![]() Make any necessary revisions to your work, and then save your work in your course folder.
Make any necessary revisions to your work, and then save your work in your course folder.
Self-Check 2
Complete Sum of Infinite Geometric Series.
There are many applications of infinite geometric series. One such application that is relevant to another area of math is converting repeating decimals into fractions.
Try This 4
- Write the number
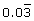 as an expanded number to 8 decimal places.
as an expanded number to 8 decimal places.
- Write this number as the sum of an infinite geometric series.

- Identify the first term and the common ratio for the series.
- Substitute the parameters into the infinite geometric series formula.
- Write an equivalent fraction for the expression in question 4. Check your answer by using a calculator to evaluate the fraction. Is the result the same as the original decimal?
- Describe how you would convert the decimal
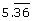 into a reduced fraction.
into a reduced fraction.
![]() Save your answers in your course folder.
Save your answers in your course folder.
Share 2
Another useful application of infinite geometric series is found in economics. If you were given the same choice as the boy in the cartoon, what would you choose?
With a classmate, discuss which option is better. Assume that the second option pays $100 at the end of each year. You may need more information before a decision can be made. Write down any additional questions that need to be asked. List one distinct advantage and one distinct disadvantage for each option. Based on your discussion, choose an option to support. Provide reasons to support your choice.
![]() Save your work in your course folder.
Save your work in your course folder.
Check with your teacher to see if you need to submit a copy for his or her review.