Lesson 1

Lesson 1 Summary

 

In this lesson you investigated the following questions:

• How can you use cosine, sine, and tangent for angles greater than 90°?
  
  
• How does the definition of cosine, sine, and tangent for angles greater than 90° affect the solution of equations?

You learned the formal definitions for the primary trigonometric ratios.

 

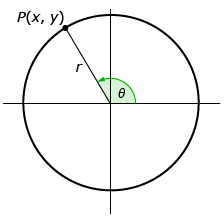
If given ∠θ drawn in standard position, with P being any point (x, y) on the terminal arm, the primary trigonometric ratios are defined as follows:

 

 

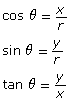
where

• x is the x-coordinate of point P

• y is the y-coordinate of point P
  
  
• r is the distance from the origin to point P

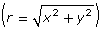
These new definitions are compatible with the right-triangle definitions you learned in your last math course. These definitions allow the use of angles greater than 90°. In Mathematics 20-1 you will only deal with 0° ≤ θ ≤ 360°; however, the formal definitions are valid for any angle.

 

This definition creates two interesting results (which you will use in Lessons 2 and 3):

• When P is on a circle of radius 1, cosine and sine are simply, and respectively, the x- and y-coordinates of P.
  
  
• Equations like cos θ = 0.2 usually have two solutions (similarly for sine and tangent).

In Lesson 2 you will learn how to solve equations like this algebraically rather than by using Primary Trigonometric Ratios: Formal Definitions.