Lesson 2

Discover

 

In Lesson 1 you used the applet Primary Trigonometric Ratios: Formal Definitions to solve equations like cos θ = 0.7. You found that there were always two answers to this equation. In previous math courses you may have found one solution to this by writing θ = cos−1(0.7) then entering cos−1(0.7) into your calculator to get the answer 46°. How do you get the second solution (314°) without having to use the applet Primary Trigonometric Ratios: Formal Definitions?

 

In Try This 1 you will explore the relationship between the answer given by your calculator and the second answer given by the applet.

 

Try This 1

 

Print three copies of Circle of Angles. You will use one copy in each part of Try This 1. Do you prefer to work digitally? If so, you can paste a screenshot of Circle of Angles into a drawing program on your computer.

 

You will be using Primary Trigonometric Ratios: Formal Definitions, which you first used in Lesson 1.

 

Part 1

 

Step 1: Use Primary Trigonometric Ratios: Formal Definitions to determine the two values of θ that make the equation cos θ = 0.309 true.

 

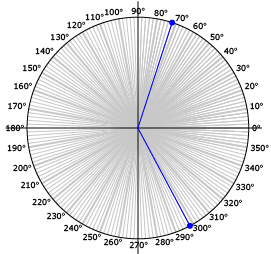
Step 2: Draw these two angles in standard position on one of the Circle of Angles worksheets you printed. Mark a large point where each terminal arm intersects the circle.

 

Step 3: Fold the worksheet along the thick horizontal line (the x-axis). Record what you notice, if anything, about the two points on the terminal arms.

 

Step 4: Fold the worksheet along the thick vertical line (the y-axis). Record what you notice, if anything, about the two points on the terminal arms.

 

Repeat Steps 1 to 4 for the following equations.

• cos θ = 0.9135
  
  
• cos θ = −0.6691
  
  
• cos θ = −0.9976

Part 2

 

Step 1: Use Primary Trigonometric Ratios: Formal Definitions to determine the two values of θ that make the equation sin θ = 0.4695 true.

 

Step 2: Draw these two angles in standard position on the second Circle of Angles worksheet you printed. Mark a large point where each terminal arm intersects the circle.

 

Step 3: Fold the sheet along the thick horizontal line (the x-axis). Record what you notice, if anything, about the two points on the terminal arms.

 

Step 4: Fold the sheet along the thick vertical line (the y-axis). Record what you notice, if anything, about the two points on the terminal arms.

 

Repeat Steps 1 to 4 for the following equations:

• sin θ = 0.9613
  
  
• sin θ = −0.9272
  
  
• sin θ = −0.4384

Part 3

 

Step 1: Use Primary Trigonometric Ratios: Formal Definitions to determine the two values of θ that make the equation tan θ = 1.8807 true.

 

Step 2: Draw these two angles in standard position on the third Circle of Angles worksheet you printed. Mark a large point where the terminal arms intersect the circle.

 

Step 3: Fold the sheet along the thick horizontal line (the x-axis). Record what you notice, if anything, about the two points on the terminal arms.

 

Step 4: Fold the sheet along the thick vertical line (the y-axis). Record what you notice, if anything, about the two points on the terminal arms.

 

Repeat Steps 1 to 4 for the following equations:

• tan θ = 0.364
  
  
• tan θ = −0.2126
  
  
• tan θ = −2.4751

Save your responses in your course folder.

 

Share 1

 

For each part of Try This 1, discuss the following questions with a partner or group.

• Does there appear to be a pattern to the relationship between each pair of angles you plotted?
  
  
• Can you see any relationship between the patterns you identified in Try This 1 and the primary trigonometric ratios introduced in Lesson 1?

Save a summary of the patterns and relationships you discussed in your course folder.

 

You will refer to your notes in Explore.